E' noto che se ad un
oggetto di massa m forniamo sufficiente velocità
v , ovvero sufficiente energia cinetica E=0.5mv2
, esso sarà in grado di allontanarsi dalla Terra e viaggiare nello
spazio.
Tuttavia la velocità finale
v' sarà inferiore a quella iniziale perché
parte dell’energia viene spesa per contrastare la forza di gravità.
Questa energia è pari a m ,
dove ,
dove  =GM/R
è l’energia potenziale terrestre che è necessaria fornire
per allontanare all’infinito un oggetto di massa unitaria; G
è la costante di gravità, e M ed R
rappresentano la massa ed il raggio della Terra. =GM/R
è l’energia potenziale terrestre che è necessaria fornire
per allontanare all’infinito un oggetto di massa unitaria; G
è la costante di gravità, e M ed R
rappresentano la massa ed il raggio della Terra.
L’energia finale sarà dunque
E' = E - m , ed avremo
v' = v (1-2 , ed avremo
v' = v (1-2 /v2)1/2. /v2)1/2.
Un fotone - l’unità elementare
della radiazione elettromagnetica - possiede caratteristiche alquanto diverse
da un corpo materiale: la sua energia non è legata alla velocità
(come accade per un oggetto materiale) ma alla sua frequenza  tramite la relazione E=h
tramite la relazione E=h , dove h è la costante di Planck.
, dove h è la costante di Planck.
Tuttavia possiamo tracciare tra il
fotone ed un corpo materiale un’approssimata ma utile analogia quando si
tenga conto che, secondo la relatività ristretta, la massa e l’energia
sono in realtà equivalenti, ed un oggetto a riposo di massa m
possiede un’energia E=mc2 , dove c
è la velocità della luce.
Possiamo allora associare al fotone
una massa m=h /c2
su cui la forza gravitazionale può esercitare la sua influenza (la
deflessione dei raggi luminosi da parte della gravità solare è
un fenomeno osservativamente documentato). Un fotone che abbandoni un corpo
di massa M e raggio R perde dunque energia.
Tale perdita non si manifesta tramite un rallentamento del fotone (la velocità
della luce è infatti una costante della natura) ma con una diminuzione
della sua frequenza, /c2
su cui la forza gravitazionale può esercitare la sua influenza (la
deflessione dei raggi luminosi da parte della gravità solare è
un fenomeno osservativamente documentato). Un fotone che abbandoni un corpo
di massa M e raggio R perde dunque energia.
Tale perdita non si manifesta tramite un rallentamento del fotone (la velocità
della luce è infatti una costante della natura) ma con una diminuzione
della sua frequenza,  '= '=  (1-
(1- /c2). Questo
effetto viene detto spostamento verso il rosso (red shift)
gravitazionale. /c2). Questo
effetto viene detto spostamento verso il rosso (red shift)
gravitazionale.
Dunque, una radiazione che si allontana
da un oggetto gravitante di potenziale  subisce una diminuzione
subisce una diminuzione   = = - - '
in ogni sua frequenza che, in termini percentuali, può essere espressa
come '
in ogni sua frequenza che, in termini percentuali, può essere espressa
come   / /  = = /c2
. /c2
.
Questa variazione è associata
ad una variazione di temperatura T dello spettro di corpo
nero che può essere compresa ricorrendo alla legge di Wien (si veda
la precedente spigolatura). Questa legge afferma che c’è una proporzione
diretta tra T e  max,
la frequenza a cui lo spettro di corpo nero ha un massimo, ovvero la frequenza
a cui l’energia elettromagnetica viene trasportata più efficacemente. max,
la frequenza a cui lo spettro di corpo nero ha un massimo, ovvero la frequenza
a cui l’energia elettromagnetica viene trasportata più efficacemente.
Se dunque T= C max,
dove C è una costante, possiamo scrivere max,
dove C è una costante, possiamo scrivere
 T/T
= T/T
=   max
/ max
/  max = max =   / /  ,
dove l’ultima uguaglianza è dovuta al fatto che la variazione percentuale
è la stessa per ogni frequenza. ,
dove l’ultima uguaglianza è dovuta al fatto che la variazione percentuale
è la stessa per ogni frequenza.
Possiamo finalmente concludere che
la temperatura di una radiazione di corpo nero che si allontana da un corpo
con potenziale  subisce una variazione subisce una variazione  T/T= T/T=  /c2
: questa relazione è nota come effetto Sachs-Wolfe, ed è
alla base delle fluttuazioni in temperatura /c2
: questa relazione è nota come effetto Sachs-Wolfe, ed è
alla base delle fluttuazioni in temperatura  T/T~10-5
della radiazione di fondo osservate sulla sfera celeste. Le dimensioni
angolari su cui si estendono queste fluttuazioni, sono legate all’età
dell’universo e alle dimensioni iniziali delle fluttuazioni in densità T/T~10-5
della radiazione di fondo osservate sulla sfera celeste. Le dimensioni
angolari su cui si estendono queste fluttuazioni, sono legate all’età
dell’universo e alle dimensioni iniziali delle fluttuazioni in densità  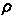 del gas cosmico in espansione.
del gas cosmico in espansione.
|