|
|
|
|
|
|
|
|
|
Fotoni preveggenti
Annibale
D’Ercole
|
Nel secolo diciottesimo, la stragrande
maggioranza degli studiosi aderiva alla teoria corpuscolare della luce di
Newton, secondo cui la radiazione consiste di un aggregato di corpuscoli
piccolissimi. La contemporanea teoria ondulatoria di Huygens poteva vantare
solo pochi sostenitori. All’inizio del secolo diciannovesimo, però, Young
scoprì che in certe circostanze due fasci di luce possono indebolirsi a
vicenda, un fenomeno assolutamente inspiegabile nella teoria corpuscolare. Il
famoso esperimento di interferenza di Young confermò inequivocabilmente la
natura ondulatoria della luce. All’inizio del ventesimo secolo, tuttavia, il
fenomeno dell’effetto fotoelettrico si mostrò refrattario a una spiegazione
basata sulla teoria ondulatoria e fu interpretato da Einstein ipotizzando una
natura corpuscolare della luce. Si è così affermato per la radiazione (ma
anche per la materia) il concetto di dualismo onda-particella. Ogni processo
può essere interpretato in termini ondulatori o corpuscolari, ma non siamo in
grado di determinare la “vera” natura della luce. Data la fondamentale
importanza dell’esperimento di Young e dell’effetto fotoelettrico nella
formulazione di questo dualismo, ne riportiamo gli aspetti salienti. L’esperimento
di Young Un fronte luminoso (che assumiamo, per
semplicità, monocromatico, ovvero composto da onde di una sola lunghezza
d’onda l, come quelle di un laser) investe un
diaframma dotato di due fenditure. Se la luce fosse composta da particelle,
esse proseguirebbero la loro traiettoria rettilinea oltre le fenditure e
andrebbero a formare due bande luminose sopra uno schermo posto oltre il diaframma.
Invece, sullo schermo compare un sistema di frange equidistanti chiare e
scure (si veda Fig. 2). Questo
si spiega ammettendo che dalle aperture del diaframma si diffondono in avanti
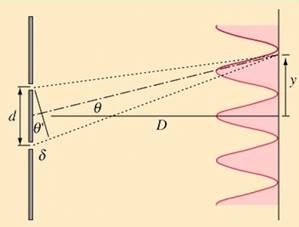
onde sferiche in grado di interferire. Consideriamo due
percorsi luminosi r1 e r2 (indicati dalle due
linee punteggiate in Fig. 5) che
partono dalle due fenditure e che giungono nel medesimo punto y dello schermo. Se la distanza D tra diaframma e schermo è molto
maggiore della distanza d tra le
due fenditure (D >> d), si ha q¢ » q
e la differenza di lunghezza d = r1 – r2 può
essere scritta come d = d sinq.
Fig. 5. Schema della
formazione di frange di interferenza nell’esperimento di Young. Si ottiene la formazione
di una frangia luminosa nel punto y
se le ampiezze delle due onde che avanzano lungo r1 e r2
interferiscono costruttivamente in y,
ovvero se la cresta (o il ventre) di una si sovrappone alla cresta (al
ventre) dell’altra. Questo avviene se d è pari a un multiplo
intero di l,
ovvero d sinq = nl,
n = 1, 2, 3, … (1) Dalla Fig. 5 si vede che tanq = y/D. Se si è posto lo
schermo a grande distanza, l’angolo q
è piccolo e vale la seguente catena di approssimazioni: tanq » sinq » q »
y/D. Dunque, in base all’eq. (1), le frange luminose si formano nei punti yn yn »
nl D/d,
n = 1, 2, 3, … Lo schermo, invece,
rimane in ombra in tutti i punti in cui convergono due tragitti la cui
differenza in lunghezza è data da un numero semintero di lunghezze d’onda, in
modo che la cresta di un’onda si sovrapponga con il ventre dell’altra dando
luogo a un’interferenza distruttiva: d sinq = (n + 0,5)l,
n=1, 2, 3, … L’effetto
fotoelettrico Se una superficie metallica viene
illuminata con luce appropriata, è possibile estrarne elettroni. È naturale
supporre che il campo elettrico della radiazione, se sufficientemente
intenso, riesca a strappare gli elettroni dall’attrazione
dei nuclei atomici del metallo e sbalzarli via. Tuttavia, le caratteristiche
dell’effetto fotoelettrico non si riescono a spiegare all’interno di uno
schema ondulatorio della radiazione elettromagnetica. Queste caratteristiche
si riassumono nei seguenti punti: 1)
la
velocità degli elettroni (e dunque la loro energia cinetica) espulsi non
dipende dall’intensità della radiazione, ma dalla sua frequenza: maggiore è
la frequenza, maggiore è la velocità; 2)
raggi
luminosi di frequenza inferiore a una certa frequenza critica ncr (che dipende dal tipo di metallo) non
sono in grado di estrarre elettroni, indipendentemente dalla loro intensità; 3)
il
numero degli elettroni estratti è proporzionale all’intensità luminosa: se
questa raddoppia, raddoppia anche quello. Ora, si intuisce
facilmente che l’energia trasportata da un’onda è legata alla sua ampiezza
(per la precisione, il quadrato dell’ampiezza): i danni provocati da una
mareggiata sono maggiori per onde con altezza maggiore. Analogamente,
l’intensità di un fascio luminoso (che assumiamo, per semplicità,
monocromatico) dipende dall’ampiezza dell’onda elettromagnetica, ovvero alla
massima intensità raggiunta dal campo elettrico (e magnetico) durante le
oscillazioni. Pertanto, ci si aspetta che un raggio luminoso più intenso
interagisca con lo stesso numero di elettroni, ma trasferendo loro una
maggiore energia, e portandoli quindi a velocità più alte. Come si vede, la
teoria ondulatoria della luce conduce a previsioni in disaccordo con i fatti
sperimentali elencati in precedenza. Nel 1905, Albert Einstein spiegò l’effetto
fotoelettrico con l’ipotesi che i raggi luminosi siano composti da particelle,
chiamate fotoni, la cui energia è direttamente proporzionale alla frequenza
della radiazione corrispondente: E =
hn, dove h è la costante di Planck e n la frequenza di
radiazione. Secondo la teoria formulata da Einstein, incidendo sulla
superficie di un corpo metallico, i fotoni cedono la propria energia agli
elettroni del conduttore, provocandone l’estrazione. Ogni elettrone acquista
un’energia cinetica K = 0,5 mu2, dove m è
la massa dell’elettrone e u la sua velocità. Questa energia è pari a K = hn – F. (2) F rappresenta il potenziale di estrazione del metallo, ovvero l’energia
che deve essere ceduta all’elettrone per svincolarlo dalla forza
elettrostatica dei nuclei atomici che lo trattiene all’interno del metallo
stesso. Si capisce dunque che l’elettrone può essere estratto solo se la
radiazione incidente ha una frequenza pari o superiore a ncr
= F/h: l’energia del fotone in eccesso rispetto al potenziale di
estrazione viene trasferita all’elettrone sotto forma di energia cinetica. È
interessante notare che l’eq. (2) può essere
utilizzata per ricavare il valore della costante di Plank. Si può infatti
ripetere l’esperimento due volte, utilizzando radiazioni di frequenze note
diverse n1 e n2, e misurare nei due casi
le energie cinetiche degli elettroni, K1
e K2. In base all’eq. (2) si ottiene pertanto h = (K1 – K2)/(n1 – n2). Secondo Einstein, dunque, l’energia dell’elettrone
liberato dipende solo dall’energia del fotone, mentre l’intensità della
radiazione è direttamente correlata al numero di fotoni trasportati dalla
radiazione e pertanto può influire sul numero di elettroni estratti dal
metallo, ma non sulla loro energia. Lo scienziato tedesco riuscì così a
spiegare tutti i fatti sperimentali concernenti l’effetto fotoelettrico e gli
fu conferito per questo il premio Nobel nel 1921. |