|
|
|
|
|
|
|
|
|
E = mc2
Annibale
D'Ercole
Osservatorio
Astronomico - Bologna
|
Per affrontare la derivazione della
formula E = mc2, è necessario prima accennare al classico fenomeno
astronomico dell’aberrazione della luce. Questo fenomeno può
essere facilmente compreso grazie a una esperienza alquanto comune nella vita
quotidiana. Supponiamo di trovarci fermi, in piedi, sotto la pioggia. In una
giornata senza vento, le gocce d’acqua cadono con velocità c, seguendo traiettorie verticali e,
per ripararci, noi dobbiamo tenere l’ombrello esattamente sopra la nostra
testa, con il bastone anch’esso in posizione verticale. Se cominciamo a
camminare con velocità -v, andiamo
incontro alla pioggia la quale ci apparirà ora avere due componenti di
velocità, una verticale c e una
orizzontale v (infatti, nel
sistema di riferimento che si muove con noi con velocità –v rispetto al precedente, noi siamo
fermi e la pioggia acquista una velocità orizzontale v verso di noi). Di conseguenza, le gocce d’acqua ci appaiono
cadere lungo traiettorie oblique e noi dobbiamo effettivamente tenere
l’ombrello inclinato in avanti, se vogliamo ripararci al meglio. Questo
effetto aumenta all’aumentare di v.
Quando ci muoviamo in macchina in una notte piovosa, la pioggia illuminata
dai nostri fari sembra provenire da zone di cielo assai più avanti rispetto a
noi.
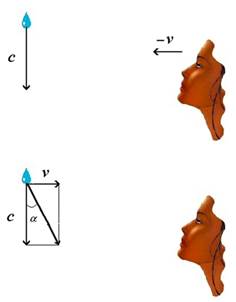
Fig. 1. Nel pannello superiore è mostrato un
osservatore che si muove con velocità –v, sotto la pioggia che cade
verticalmente con velocità c. Nel pannello inferiore, la stessa
scena è mostrata come appare in un sistema di riferimento che si muove con
l’osservatore. In questo riferimento, l’osservatore è fermo e la pioggia
acquista una componente orizzontale di velocità v e la sua traiettoria
appare inclinata di un angolo α rispetto alla verticale. L’effetto appena
descritto vale anche per i raggi luminosi. Se una stella si trova allo zenit,
ossia proprio sopra di noi, i suoi raggi luminosi dovrebbero apparire
perfettamente verticali e anche il tubo del telescopio dovrebbe essere
posizionato verticalmente per inquadrare la stella. Dal momento, però, che Il lettore che ha avuto
la pazienza di seguirci fin qui si chiederà cosa c’entri tutto quello che
abbiamo detto finora con l’equivalenza tra massa ed energia, che rimane
l’argomento di discussione di questa nota. In effetti, è una caratteristica
del genio di Einstein quella di dimostrare cose straordinarie tramite
esperimenti mentali all’apparenza banali e scollegati dall’argomento che si
vuol trattare. Quella che segue è l’ultima delle varie dimostrazioni che
Einstein ha dato della sua celebre formula. Supponiamo di avere un
oggetto di massa M, ad esempio un
libro, posto in quiete al centro tra due lampadine i cui raggi luminosi
colpiscono il libro stesso. I fotoni emessi dalle lampadine hanno ognuno
energia 0.5E, sicché, ogni volta
che il libro è colpito (simultaneamente) da due fotoni, si scalda aumentando
la sua energia di una quantità E.
Già da moltissimo tempo gli astronomi sono a conoscenza del fatto che la luce
esercita una pressione; le code delle comete si pongono sempre in direzione
opposta a quella del Sole, proprio perché sono “soffiate via” dalla radiazione
solare. La pressione esercitata da un fotone su, diciamo, un elettrone può
essere intesa come un trasferimento di quantità di moto dal fotone
all’elettrone. Sperimentalmente, si trova che la quantità di moto di un
fotone è pari a q = E/c, dove E è l’energia del fotone e c è la velocità della luce[1].
Tornando al nostro libro, esso, essendo sottoposto a due pressioni di
radiazione laterali uguali e contrarie, rimane fermo.
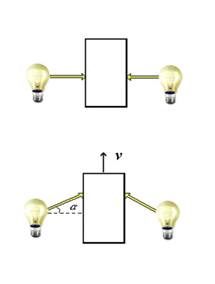
Fig. 2. Nel pannello superiore è mostrato il
libro in quiete, posto a metà strada tra due lampadine i cui raggi luminosi
lo illuminano orizzontalmente. Nel pannello inferiore, il libro è mostrato
come appare da un sistema di riferimento in moto verso il basso con velocità –v;
in questo riferimento il libro appare muoversi verso l’alto con velocità v
e i raggi luminosi risultano inclinati di un angolo α rispetto
all’orizzontale. Poniamoci ora in un
sistema di riferimento che si muova verso il basso con velocità –v (si veda la fig. 2). Il libro ci
apparirà muoversi verso l’alto con velocità v. Ma questa non è l’unica differenza; a causa del fenomeno
dell’aberrazione della luce, i fotoni provenienti dalle lampadine colpiscono,
ora, il libro obliquamente e gli cedono la componente verticale della loro
quantità di moto. Questa addizione di quantità di moto non può andare a
incrementare la velocità del libro portandola ad un valore v’ > v. Se così fosse, tornando al riferimento iniziale il libro non
ci apparirebbe fermo, ma dotato di una velocità verso l’alto v’ - v. Questo però non può essere perché nulla giustifica, in questo
riferimento, l’acquisizione di una simile velocità da parte del libro.
L’unico modo per aumentare la quantità di moto del libro senza variarne la
velocità è ammettere che ad aumentare sia la sua massa, che diventa M’ > M. Tenuto conto che ciascun
fotone cede al libro la sua componente verticale di quantità di moto pari a
0.5 sin(α)E/c ≈ 0.5Ev/c2 (per il seno vale ciò che è vero per la tangente
ovvero il suo valore è assai simile a quello dell’angolo stesso quando
quest’ultimo è molto piccolo), dalla conservazione della quantità di moto
abbiamo allora: M’v
= Mv + Ev/c2. Dividendo tutti i membri
per v e ponendo m = M’ - M, possiamo finalmente scrivere E
= mc2. In altri termini,
l’energia dei fotoni assorbita (sotto forma di calore) dal libro va ad
aumentare la massa del libro stesso. Questo risultato non vale solo per
l’energia elettromagnetica, ma ha carattere generale e sancisce l’equivalenza
tra la massa e qualunque forma di energia. Una conseguenza
clamorosa dell’equivalenza tra massa ed energia è data dalla realizzazione
delle reazioni nucleari. In particolare, la fusione dei nuclei di idrogeno,
ossia i protoni, fornisce l’energia che permette al Sole di risplendere da
4,5 miliardi di anni e gli permetterà di farlo in futuro per un analogo lasso
di tempo. L’alta densità (150 g/cm3) e temperatura (15.000.000 K) al
centro del Sole permettono a due protoni di superare la repulsione
elettrostatica e fondersi assieme a due neutroni formando nuclei di elio,
ciascuno costituito, appunto, da due protoni e due neutroni. Ora, se
potessimo pesare il nucleo di un atomo di elio, di massa mHe, ci accorgeremmo che è più leggero della somma dei
suoi quattro componenti. In particolare, considerando che la massa di un
neutrone è sostanzialmente uguale a quella del protone mp, si trova che 4mp
- mHe = 0.029mp, con una percentuale di
massa persa pari a (4mp -
mHe)/4mp ≈ 0,007. Dunque,
la trasmutazione dell’idrogeno in elio include una perdita di massa di circa Anche se la massa
mancante è piccola, l’energia prodotta è grande (grazie al grande valore di c), circa 6×1018 erg per
ogni grammo di materia annichilita. Dal momento che la massa di idrogeno nel
Sole ammonta a circa il 70% di quella totale (pari a M = 2×1033 g), le riserve di combustibile nucleare
potrebbero permettere al Sole, nel corso della sua esistenza, di produrre una
quantità di energia pari a Eto
t= 0,007 × 0,7 × Mc2=8,82 × 1051 erg. Poiché il Sole perde
energia ad un tasso pari alla sua luminosità L = 4 × 1033 erg/s, in linea di principio esso può
splendere per un periodo pari a t =
Etot/L ≈ 100 miliardi di anni. In
verità, solo un decimo dell’idrogeno del Sole, quello che si trova nelle zone
centrali, dove le condizioni sono favorevoli all’innesco delle reazioni
nucleari, è destinato a trasformarsi in elio; la vita del Sole si riduce
pertanto a t = 10 miliardi di
anni, un lasso di tempo comunque ampiamente sufficiente a permettere l’evoluzione
sulla Terra! |