E' noto che la pressione esercitata da un gas contro le pareti del
recipiente che lo contiene è dovuta agli urti continui degli atomi che lo compongono
contro tali pareti.
In termini microscopici la pressione viene definita come
e mostra come essa è tanto maggiore quanto maggiore è la densità n
e/o la velocità v degli atomi di massa m.
E' altresì possibile risalire alla velocità degli atomi tramite la misura di una
quantità macroscopica del gas - la sua temperatura - definita, a parte fattori numerici
inessenziali, come T~mv2/k, dove k
è una costante della natura, detta costante di Boltzmann.
In conclusione, la pressione di un gas si può scrivere come
Questa è una ben nota espressione della termodinamica che vale per
un gas in condizioni ordinarie, quali quelle che si trovano all’interno delle stelle
durante la fase attiva della loro esistenza, ovvero fino a quando al centro sono attive le
reazioni nucleari che sviluppano energia.
Questa energia porta la temperatura del gas al centro a valori alquanto elevati (diverse
centinaia di milioni di gradi). Di conseguenza, anche la pressione centrale del gas
è molto alta ed in grado di controbilanciare il peso degli strati superiori della stella,
stabilendo così l’equilibrio idrostatico. In altre parole, il peso della stella
impedisce alla pressione di gonfiarla fino a dissolverla e, viceversa, la pressione si
oppone all’azione della gravità che tende a comprimere la stella a densità
inimmaginabili e dimensioni ridottissime.
Dopo diversi miliardi di anni, tuttavia, il combustibile nucleare si esaurisce e
l’equilibrio idrostatico si spezza. La pressione del gas, non più sostenuta
dallo sviluppo di energia nucleare, non è più in grado di controbilanciare il peso della
stella che quindi è destinata a contrarsi sempre più.
Le osservazioni, tuttavia, mostrano che la stella smette di contrarsi stabilizzandosi come
nana bianca su una nuova configurazione di equilibrio. Il Sole, che
attualmente ha un raggio di 700 000 km, è destinato a diventare una nana bianca con un
raggio di tipo planetario, oltre cento volte più piccolo, raggiungendo densità enormi,
dell’ordine di alcune decine di milioni di grammi per centimetro cubo.
A queste densità la materia smette di trovarsi in condizioni ordinarie e diventa degenere.
L’espressione per la pressione considerata finora [equazione (2)] non è
più valida, e bisogna ricorrere alla meccanica quantistica per una corretta descrizione
della pressione che stabilizza la nana bianca.
La teoria quantistica stabilisce che gli elettroni sono soggetti ad una
importante restrizione nota come Principio di Esclusione di Pauli; tale principio
impedisce che due elettroni abbiano proprietà identiche. Questo vale
anche per neutroni, protoni, neutrini e tutti gli altri Fermioni, ovvero per tutte le
particelle il cui spin (una quantità legata alla velocità di rotazione di una particella
su se stessa) assume valori seminteri della costante di Planck (1/2 h,
3/2 h, ...).
In meccanica quantistica, tuttavia, bisogna essere cauti nel definire l’identità di
due elettroni. Chiaramente possiamo sempre immaginare una differenza estremamente
piccola nella velocità o nella posizione di due elettroni.
Ci chiediamo quando tale differenza è così piccola da permettere di definire i due
elettroni identici. A questa domanda risponde il Principio di Indeterminazione
di Heisenberg, che nega la possibilità di distinguere due particelle se la loro
differenza di impulso  p (definito
come p=mv ), moltiplicato per la differenza in posizione p (definito
come p=mv ), moltiplicato per la differenza in posizione  r, è minore
della costante di Planck h. r, è minore
della costante di Planck h.
Più precisamente, per ogni direzione spaziale deve valere:
 px px  x = h , x = h ,  py py  y = h , y = h ,  pz pz  z = h. z = h.
In un’unica formula, il Principio di Heisenberg può essere scritto come
 V V  p3 = h3 p3 = h3
|
( 3 ) |
dove  V= V= x x  y y  z e z e
 p3 = p3 =
 px px
 py py
 pz
, e stabilisce che è impossibile operare misure di velocità e posizione di una
particella che siano prive di incertezza (questa incertezza è intrinseca nella natura e
non è legata alla nostra abilità nella misura). pz
, e stabilisce che è impossibile operare misure di velocità e posizione di una
particella che siano prive di incertezza (questa incertezza è intrinseca nella natura e
non è legata alla nostra abilità nella misura).
Dunque, contrariamente al mondo macroscopico a cui siamo abituati, nel mondo subatomico la
nozione di posizione di una particella è priva di significato. In realtà è
possibile risalire soltanto alla probabilità di trovare la particella in una
determinata regione ed individuare un volume  V all’interno del quale tale probabilità è
alta. V all’interno del quale tale probabilità è
alta.
Se dunque la densità della stella collassante si fa alta al punto che un numero N
di elettroni vengano a trovarsi all’interno del volume  V, tali elettroni risultano
spazialmente indistinguibili nel senso che non è possibile capire a quale elettrone in
entrata in V, tali elettroni risultano
spazialmente indistinguibili nel senso che non è possibile capire a quale elettrone in
entrata in  V
corrisponda un determinato elettrone in uscita. V
corrisponda un determinato elettrone in uscita.
Per il Principio di Pauli tali elettroni devono allora avere impulsi differenti.
Se il primo elettrone ha impulso compreso tra 0 e  p3 (0 p3 (0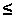 p3 p3 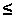  p3),
il secondo lo dovrà avere nell’intervallo p3),
il secondo lo dovrà avere nell’intervallo  p3 p3 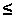 p3 p3 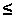 2 2 p3,
il terzo nell’intervallo 2 p3,
il terzo nell’intervallo 2 p3 p3 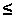 p3 p3 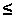 3
3 p3, e così
via fino all’ultimo per cui (N - 1) p3, e così
via fino all’ultimo per cui (N - 1) p3 p3 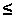 p3 p3 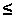 N N p3. p3.
Dunque il massimo impulso presente è pm3 = N (  p )3 , che si può
anche scrivere, tenendo conto dell’equazione (3), pm=hn1/3
, dove n=N/ p )3 , che si può
anche scrivere, tenendo conto dell’equazione (3), pm=hn1/3
, dove n=N/  V
è la densità degli elettroni. V
è la densità degli elettroni.
A questo punto, ricordando la definizione di pressione [equazione (1)] e di impulso,
otteniamo l’espressione per la pressione degli elettroni P = (h2/m)n5/3
.
Una trattazione più rigorosa fornisce l’espressione esatta:
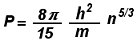
|
( 4 ) |
L’equazione (4) descrive la pressione elettronica nel caso
degenere - detta pressione di Fermi -, ed è utile confrontarla con
l’equazione (2) valevole nel caso ordinario di basse densità.
La pressione di Fermi non dipende dalla temperatura (e dunque dalle reazioni nucleari) ma
solo dalla densità e diventa importante solo per valori elevati di quest’ultima.
Inoltre, la pressione di Fermi è inversamente proporzionale alla massa delle
particelle.
Per questo motivo in questa nota si è insistito sugli elettroni; la loro massa, infatti,
è circa duemila volte più piccola di quella dei protoni la cui pressione di Fermi è
pertanto trascurabile.
|