E' noto che un corpo caldo emette radiazione
tramite gli atomi che lo compongono.
La radiazione atomica, d’altro canto, è prodotta dagli elettroni il cui moto
all’interno di un atomo può essere assimilato, ai fini dello studio della radiazione
emessa, ad un’oscillazione avanti e indietro rispetto al nucleo.
Ad un oggetto in movimento è associata un’energia – l’energia cinetica
-- che cresce all’aumentare della sua velocità: un bersaglio riceve un danno
maggiore se raggiunto da un proiettile sparato con una pistola piuttosto che scagliato,
diciamo, con una fionda, perché nel secondo caso la velocità, e dunque l’energia in
gioco, è minore.
Nel caso dell’oscillazione di un elettrone all’interno di un atomo (oscillatore
atomico) la rapidità del moto, e di conseguenza la sua energia cinetica E
, è misurata dalla frequenza  che
è anche la stessa frequenza della radiazione emessa. che
è anche la stessa frequenza della radiazione emessa.
Dal momento che l’energia trasportata da un’onda elettromagnetica è legata
all’energia dell’elettrone che l’ha emessa, si ricava che l’energia
della radiazione è tanto maggiore quanto maggiore è la sua frequenza: i raggi infrarossi
sono meno energetici di quelli ultravioletti perché la loro frequenza è minore (o,
equivalentemente, la loro lunghezza d’onda 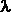 è maggiore, dal momento che vale la relazione è maggiore, dal momento che vale la relazione 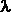 = c / = c /  , dove c è la
velocità della luce). , dove c è la
velocità della luce).
Se si agita una scatola piena di palline, queste acquisiscono una velocità che non è
uguale per tutte, alcune essendo più veloci, e dunque più energetiche, di altre. È
possibile tuttavia definire un’energia media rappresentativa del moto delle palline
nel loro insieme: all’aumentare dell’agitazione della scatola l’energia
media aumenta. Analogamente, se, fornendo calore, un oggetto viene portato alla
temperatura T , gli elettroni all’interno degli atomi
acquisiscono diverse frequenze e quindi diverse energie cinetiche E
la cui media è data da 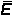 . .
Se la temperatura aumenta, le velocità di oscillazione crescono, e così pure 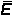 . Dal momento che l’intensità
dell’irraggiamento cresce al crescere dell’energia degli elettroni, questo
spiega la comune esperienza che ogni corpo riscaldato emette una radiazione (si pensi al
filamento di una lampadina) la cui intensità aumenta all’aumentare della
temperatura. Ma l’incremento di luminosità non è l’unico effetto associato
alla crescita della temperatura. All’aumentare delle energie degli elettroni viene
emessa radiazione che si estende fino a frequenze maggiori, e l’oggetto scaldato
cambia colore. Quando cominciamo a scaldare il filamento di una stufa elettrica, esso
effettivamente non emette radiazione visibile, ma emana calore tramite radiazione
infrarossa. All’aumentare della temperatura la potenza irraggiata aumenta, e il
filamento dapprima assume un colore rosso cupo per poi passare ad un arancione vivo, dal
momento che l’arancione corrisponde a radiazione di lunghezza d’onda minore
rispetto al rosso e all’infrarosso. . Dal momento che l’intensità
dell’irraggiamento cresce al crescere dell’energia degli elettroni, questo
spiega la comune esperienza che ogni corpo riscaldato emette una radiazione (si pensi al
filamento di una lampadina) la cui intensità aumenta all’aumentare della
temperatura. Ma l’incremento di luminosità non è l’unico effetto associato
alla crescita della temperatura. All’aumentare delle energie degli elettroni viene
emessa radiazione che si estende fino a frequenze maggiori, e l’oggetto scaldato
cambia colore. Quando cominciamo a scaldare il filamento di una stufa elettrica, esso
effettivamente non emette radiazione visibile, ma emana calore tramite radiazione
infrarossa. All’aumentare della temperatura la potenza irraggiata aumenta, e il
filamento dapprima assume un colore rosso cupo per poi passare ad un arancione vivo, dal
momento che l’arancione corrisponde a radiazione di lunghezza d’onda minore
rispetto al rosso e all’infrarosso.Benché il
quadro appena descritto si applichi a tutti gli oggetti, ci si aspetta che corpi di
sostanze diverse, anche se posti alla stessa temperatura, presentino qualche differenza
nella radiazione emessa perché diversi sono gli atomi che li compongono e diverse sono le
loro modalità di oscillazione (si pensi alla diversità di oscillazione di una molla di
orologio e di una molla utilizzata come ammortizzatore di un’automobile). In effetti
queste differenze ci sono. Tuttavia, fin dal 1792, T. Wedgwood, famoso per le sue
porcellane e antenato di Darwin, aveva osservato che tutti i corpi diventano rossi roventi
alla stessa temperatura. In realtà c’è una condizione particolare in cui tutti i
corpi, indipendentemente dalla natura, emettono la stessa radiazione: questa condizione è
detta equilibrio termodinamico.
Una reale comprensione dell’equilibrio termodinamico
si ottiene solo tramite la meccanica quantistica.
Tuttavia possiamo farci un’idea di cosa si tratta ricorrendo di nuovo
all’esempio di un "gas" di palline all’interno di una scatola.
Supponiamo di agitare la scatola in una sola direzione, per esempio destra-sinistra. Le
palline cominceranno a muoversi nella stessa direzione. Tuttavia, dopo ripetuti urti tra
loro e con le pareti della scatola, esse si muoveranno anche nella direzione ortogonale,
avanti-indietro.
Alla fine acquisiranno una precisa distribuzione di velocità in tutte le direzioni,
alcune essendo più veloci ed altre più lente, con energia media 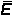 . .
Se agitassimo la scatola nella sola direzione avanti-dietro, dopo un numero sufficiente di
urti la distribuzione di velocità delle palline sarebbe la stessa del caso precedente.
Più in generale, la distribuzione in velocità ed energia è sempre la stessa
indipendentemente da come forniamo energia al sistema di palline, purché si realizzi un
numero elevato di urti.
Ora, un oscillatore atomico si comporta come un’antenna radio: non solo è in grado
di emettere radiazione, ma anche di riceverla, o, per meglio dire, di assorbirla.
Un’onda elettromagnetica che colpisce un oscillatore atomico comunica un moto
oscillatorio, e dunque un’energia cinetica, all’elettrone a spese della propria
energia. La radiazione, dunque, viene assorbita, totalmente o parzialmente, dagli atomi
che a loro volta riemettono radiazione.
All’interno dei forni di Wedgewood (e di tutti gli altri forni) la radiazione emessa
dalle pareti, poste ad una determinata temperatura, interagisce una moltitudine di volte
con gli atomi delle pareti stesse, venendo continuamente assorbita e riemessa.
Analogamente all’urto tra palline, questo fenomeno fa sì che la distribuzione in
energia – ovvero in frequenza – della radiazione non dipenda dalla particolare
struttura atomica delle pareti.
Considerazioni termodinamiche mostrano che le proprietà della radiazione emessa da un
corpo in equilibrio termodinamico non dipendono dalla specifica composizione o
peculiarità del corpo emittente, ma unicamente dalla sua temperatura. Proprio questa
estrema generalità rende di fondamentale importanza questa radiazione, detta radiazione
di corpo nero (questo nome deriva dalla proprietà di un corpo ideale posto in
equilibrio termodinamico di assorbire completamente la radiazione di qualunque frequenza).
In particolare, molte sorgenti astronomiche, a partire dalle stelle, emettono radiazione
con caratteristiche molto simili a quella di corpo nero. Infatti la radiazione stellare è
prodotta al centro dell’astro, dove avvengono le reazioni nucleari. Prima di
raggiungere la superficie stellare e disperdersi nello spazio, un raggio luminoso
"urta" con gli atomi della stella circa 1022 (diecimila miliardi di
miliardi) volte procedendo a zig-zag ed impiegando, nonostante si propaghi a 300,000
chilometri al secondo, diverse migliaia di anni per attraversare un raggio stellare, circa
1,000,000 di chilometri. Dopo tutti questi urti la radiazione stellare approssima bene la
radiazione di corpo nero.
Fu Max Planck nel 1900 a fornire la formula che descrive
esattamente la potenza emessa da un’unità di superficie di un corpo nero, e che va
sotto il nome di legge di Planck:
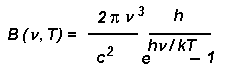
In questa formula h e k
sono, rispettivamente, la costante di Planck e la costante di Boltzmann, e  rappresenta la frequenza della radiazione.
L’energia irraggiata non è monocromatica, ma viene emessa a tutte le frequenze.
Infatti, come abbiamo già detto, gli elettroni non oscillano all’unisono tutti alla
stessa frequenza; questa differenziazione porta ad una molteplicità di frequenze delle
onde elettromagnetiche prodotte. rappresenta la frequenza della radiazione.
L’energia irraggiata non è monocromatica, ma viene emessa a tutte le frequenze.
Infatti, come abbiamo già detto, gli elettroni non oscillano all’unisono tutti alla
stessa frequenza; questa differenziazione porta ad una molteplicità di frequenze delle
onde elettromagnetiche prodotte.
La distribuzione in frequenza – o, come si dice, la distribuzione spettrale
– della radiazione di corpo nero ottenuta in laboratorio è perfettamente descritta
dalla legge di Planck.
La potenza totale emessa per unità di superficie si ottiene sommando i contributi della
radiazione di tutte le frequenze.
Si ottiene in questo modo la legge di Stefan F = a T4
, dove a è la costante di Stefan. Questa legge, già
nota prima di Planck, dà la dipendenza dell’emissione dalla temperatura del corpo
nero: ad esempio, raddoppiando la temperatura la potenza emessa aumenta di 16 volte.
Un’altra proprietà della radiazione di corpo nero, anch’essa già nota ai tempi
di Planck, è data dalla legge di Wien 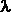 max T = C , dove C
è una costante ricavabile sperimentalmente e max T = C , dove C
è una costante ricavabile sperimentalmente e 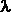 max è la lunghezza d’onda a
cui cade il massimo di emissione. max è la lunghezza d’onda a
cui cade il massimo di emissione.
Dalla formula di Planck si può riottenere in modo naturale
questa relazione che vincola la lunghezza d’onda del massimo di emissione alla
temperatura: all’aumentare di quest’ultima il grosso dell’emissione avviene
a lunghezze d’onda via via decrescenti.
Le leggi di Stefan e Wien quantificano quanto è riscontrabile nell’esperienza
quotidiana, come abbiamo visto nell’esempio del filamento della stufa elettrica.
Si è già accennato all’inizio come la legge di
Planck trovi vasto utilizzo in astrofisica. Mediante osservazioni spettroscopiche (ovvero
misurazioni di luminosità a diverse frequenze) di una sorgente è possibile ricostruirne
lo spettro e risalire a 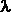 max,
e poi dedurre la temperatura tramite la legge di Wien. Se poi è nota la distanza d
della sorgente, dalla luminosità apparente l si
ricava la luminosità assoluta L = l / 4 max,
e poi dedurre la temperatura tramite la legge di Wien. Se poi è nota la distanza d
della sorgente, dalla luminosità apparente l si
ricava la luminosità assoluta L = l / 4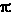 d2. d2.
Dal momento che L = SF, tramite la legge di Stefan è
possibile calcolare F e risalire alla superficie S,
e dunque alle dimensioni, della sorgente.
Accanto alla larga applicabilità dell’emissione di
corpo nero, la sua straordinaria importanza risiede nel fatto che, per arrivare alla sua
spiegazione, Planck fu indotto, dopo anni di tentativi, ad ipotizzare che le frequenze con
cui oscillano gli elettroni non possono assumere valori qualunque, ma solo valori multipli
di una frequenza fondamentale  o
, ossia o
, ossia  o, 2 o, 2 o, 3 o, 3 o, ecc. o, ecc.
Un recipiente pieno d’acqua può essere svuotato con continuità ed alleggerito del
peso desiderato agendo opportunamente sul rubinetto. Ma se il recipiente è pieno di
mattoni tutti uguali, esso può essere alleggerito di una quantità che non può essere
qualunque, ma pari ad un multiplo intero del peso di un mattone.
Analogamente, la radiazione emessa da un atomo non può essere qualunque, ma è quantizzata.
In effetti l’emissione degli atomi non si estende su tutte le frequenze, ma avviene
solo per alcune frequenze dette righe.
Per un singolo atomo queste righe sono alquanto separate in frequenza l’una
dall’altra. Nelle molecole, dove gli atomi sono "impacchettati’’, le
righe sono molto più accostate. Nei solidi questa tendenza è rafforzata e le righe si
sovrappongono tra loro dando luogo alla distribuzione spettrale continua data dalla legge
di Planck.
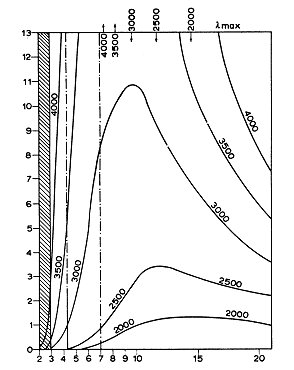 
A sinistra: distribuzione spettrale dell'intensità
della radiazione termica secondo Planck, per temperature da 2000 a 4000 °K. Le
temperature, in gradi kelvin, sono indicate sulle curve corrispondenti. L'unità in
ascissa è 0,1 m (1 m è uguale a 10-6 m). La parte tratteggiata corrisponde
alla regione dell'ultravioletto fino a 0,28 m ; la regione del visibile è quella fra le
due punteggiate.
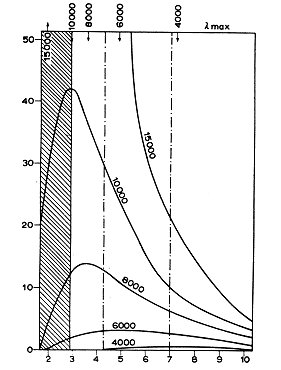
A destra: lo stesso che nell'altra figura, ma per temperature più elevate, da 4000
a 15000 °K. L'unità sull'asse delle ordinate è più piccola di quella della figura a
sinistra.
(Da Max Born, Fisica atomica, settima edizione, Boringhieri, 1968)
|