Dall’elettromagnetismo classico sappiamo
che un elettrone di carica - e sottoposto ad
un’accelerazione a irraggia una energia per unità
di tempo pari a W=2e2a2/3c3
, dove c è la velocità della luce (si veda la
precedente Spigolatura).
Nel caso di un elettrone che oscilli attorno ad una posizione fissa (come è lecito
schematizzare, ai fini di questo problema, il moto di un elettrone in un atomo), è
possibile esprimere l’accelerazione in funzione della frequenza di oscillazione  e dell’energia cinetica E=0.5
mv2 , dove m è la massa
dell’elettrone e v la sua velocità. e dell’energia cinetica E=0.5
mv2 , dove m è la massa
dell’elettrone e v la sua velocità.
Tralasciando i dettagli matematici, peraltro non difficili, si ottiene (trascurando per
semplicità le quantità costanti) W   2E. 2E.
Un corpo di dimensioni macroscopiche è composto da un numero enorme di atomi, ognuno
assimilabile ad un oscillatore con una propria frequenza ed una propria energia. Il flusso
di radiazione B di frequenza  emesso dall’unità di superficie è dato
dal contributo W di ogni oscillatore. Si ottiene emesso dall’unità di superficie è dato
dal contributo W di ogni oscillatore. Si ottiene 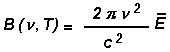
dove 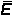 è l’energia mediata su tutti gli oscillatori. Proprio il calcolo di questa
energia media risulta cruciale per la corretta valutazione di B.
è l’energia mediata su tutti gli oscillatori. Proprio il calcolo di questa
energia media risulta cruciale per la corretta valutazione di B.
Supponiamo che uno studente, in tre successive interrogazioni, realizzi le seguenti
votazioni: v1=9, v2=5, v3=4. Se
il voto finale è dato in base alla media aritmetica, allora si avrà
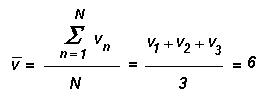
Qui N rappresenta il numero
di interrogazioni ed il simbolo di sommatoria 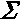 è utilizzato per esprimere in maniera
compatta una sequenza di numerosi addendi. Dunque, il nostro studente, nonostante il
vistoso calo di rendimento, raggiunge ugualmente la sufficienza. è utilizzato per esprimere in maniera
compatta una sequenza di numerosi addendi. Dunque, il nostro studente, nonostante il
vistoso calo di rendimento, raggiunge ugualmente la sufficienza.
Supponiamo ora che il professore ritenga le interrogazioni successive più significative
di quelle precedenti in quanto riguardano una fetta più ampia del programma scolastico e
danno quindi una valutazione più realistica dell’effettiva preparazione dello
studente. Ogni voto viene allora pesato moltiplicandolo per un "peso" p
che, per esempio, può essere fatto nel seguente modo: p1=1/3,
p2=2/3, p3= 3/3.
Il voto finale si ottiene tramite la media pesata
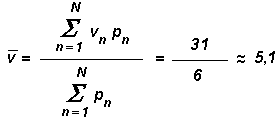
e lo studente viene bocciato.
La media aritmetica è un caso particolare di media pesata, in cui tutti i pesi sono pari
all’unità. In natura le medie pesate si realizzano comunemente. All’interno di
un gas ad una determinata temperatura si trovano atomi con qualunque velocità, ma atomi
con velocità alte sono più rari. Analogamente, gli elettroni degli atomi che compongono
un corpo posto a temperatura T possono oscillare con
qualunque frequenza, ma quelli che vibrano a bassa frequenza – e quindi con bassa
energia – sono più numerosi. Dunque l’energia media tra tutti gli oscillatori
non si realizza tramite una media aritmetica, ma si può dimostrare che il contributo di
un oscillatore di energia E viene pesato tramite il peso p=e
-E/kT tanto più grande quanto più piccolo è E.
Contrariamente al numero di interrogazioni, che è dato da un numero intero che può
aumentare di un’unità alla volta (non esiste un terzo, un quarto di
interrogazione!), si può andare da una frequenza all’altra passando per tutti i
valori intermedi (anche non interi). La media in questo caso va calcolata tramite un
integrale e non una sommatoria:
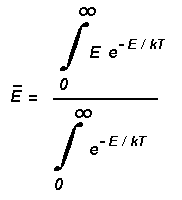
Questa formula può calcolarsi facilmente con gli usuali
metodi di analisi matematica, e si ottiene 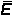 =kT. Adottando questo valore dell’energia
media, l’espressione che si ottiene per il flusso B( =kT. Adottando questo valore dell’energia
media, l’espressione che si ottiene per il flusso B( ,T) ,T)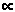  2T
è chiaramente contraddittoria. 2T
è chiaramente contraddittoria.
Se fosse vera un corpo nero emetterebbe energie sempre maggiori al crescere della
frequenza. La potenza totale emessa, derivante dal contributo di tutte le frequenze,
risulterebbe infinita. Questo paradosso era noto col nome di "catastrofe
ultravioletta".
Planck si dedicò per anni a questo problema tentando di risolverlo rimanendo nella
cerchia delle idee classiche. Infine, dopo ripetuti insuccessi, avanzò l’audace
ipotesi che un oscillatore atomico non possa vibrare con qualunque energia, ma solo con
"quanti" finiti, discreti di energia Eo ;
l’energia dell’oscillatore deve essere uguale o a Eo,
o a 2Eo, o a 3Eo,
e così via.
L’energia media si ottiene allora sommando tutte queste energie ognuna con il suo
peso, in maniera analoga al calcolo del voto medio pesato nell’esempio dato più
sopra. In questo caso la sommatoria è composta da un numero infinito di addendi, ma il
risultato finale è comunque un numero finito, e non infinito, perché i pesi pn=e-nEo/kT
degli addendi successivi diventano rapidamente sempre più piccoli al crescere di n.
L’energia media diventa allora
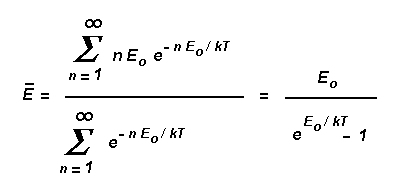
Planck utilizzò questa formula nel calcolo del flusso; per
accordarsi con la legge dello spostamento di Wien egli pose Eo=h , dove h è una
costante universale (costante di Planck). , dove h è una
costante universale (costante di Planck).
Il risultato finale è la legge di Planck della radiazione di corpo nero
|