|
|
|
|
|
|
|
|
|
La distanza delle stelle
Claudio
Elidoro
|
Lasciato alle
spalle il faticoso cammino che ci ha portati alla determinazione delle
distanze della Luna e del Sole (vedi: Spigolature
in «Giornale di Astronomia», 35 (2), 2009 e 36 (2) 2010), possiamo completare
il nostro percorso dedicandoci alla misurazione della distanza delle stelle. Non
è così immediato pensare che le stelle possano trovarsi a distanze
differenti: l'osservazione della cupola stellata proprio non ci dà il minimo
appiglio per ragionare in tal senso. Al massimo, notando nel corso del tempo
i loro evidenti spostamenti rispetto allo sfondo, possiamo correttamente
ritenere una manciata di astri più prossimi di tutti quanti gli altri, ma
nulla più. Questa constatazione risale ai primordi della scienza astronomica,
quando gli antichi scrutatori dei cieli avevano chiaramente distinto quei
puntini più irrequieti da tutti gli altri. Perché la cosa fosse ancora più
chiara venne dai greci introdotto il termine “pianeta”, derivandolo dal verbo
πλανάω
che significa errare, vagabondare. Ma della distanza delle stelle non si
sapeva proprio nulla. L'esperienza
comune ci può dare un eccellente appiglio per proporre un metodo efficace. Se
stendiamo un braccio tenendo tra le mani una matita e chiudiamo prima un
occhio e poi l'altro, notiamo che la matita oscilla tra due posizioni
rispetto agli oggetti di sfondo. Il fenomeno prende il nome di parallasse,
termine che deriva dal greco παράλλαξις il
cui significato originario era “accavallamento”. Ipotizzando il moto della
Terra intorno al Sole, osservazioni effettuate a sei mesi di distanza – cioè
con la Terra in due posizioni opposte della sua orbita – potevano permettere
di individuare le stelle più vicine rispetto a quelle molto più lontane (Fig. 1).
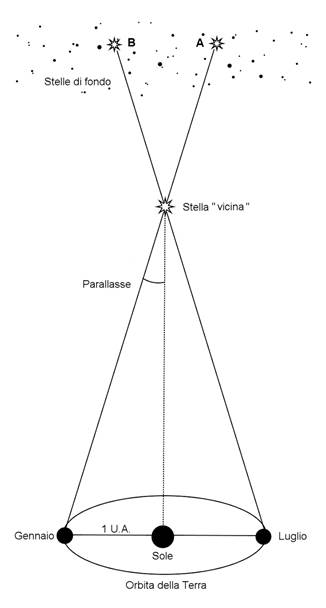
Fig. 1. La variazione di
posizione della Terra a distanza di sei mesi permette di rilevare l'apparente
spostamento di una stella rispetto a quelle di fondo. Se l'osservatore, in
gennaio, rispetto alle stelle di fondo cielo, vede la stella nella posizione A,
sei mesi più tardi potrà osservare che si è spostata in B. Dal punto
di vista geometrico, la parallasse è l'angolo sotto cui dalla stella viene
sottesa la distanza Terra-Sole. Conoscendo dunque quest'ultima, si può
risalire agevolmente alla distanza della stella. Scegliendo poi
opportunamente l'unità di misura, è possibile stabilire una semplice relazione
tra distanza e parallasse. Chiamando parsec la distanza alla quale 1 ua viene
sottesa da una parallasse di 1 arcosecondo, la
distanza (in parsec) di una stella con parallasse p (in arcsec) risulta essere: d = 1
/ p. Si noterà come non vi compaia alcuna funzione trigonometrica:
l'estrema esiguità degli angoli in gioco autorizza infatti a confondere il
valore della tangente con quello dell'arco. La semplicità della relazione ha
fatto sì che gli astronomi in genere prediligano il parsec all'anno luce. Ora
sappiamo che un simile metodo richiede misurazioni strumentali estremamente
accurate e che era assolutamente impraticabile con i mezzi osservativi di cui
potevano disporre gli antichi astronomi. Questo spiega come mai la
misurazione della parallasse rimase un autentico miraggio per molti secoli. E
non ce la sentiamo proprio di escludere che – oltre ovviamente alle ben note
motivazioni filosofiche e religiose – una delle ragioni che ostacolarono
l'idea della Terra in moto attorno al Sole non possa essere stata proprio
l'impossibilità di notare il benché minimo cambiamento nella sfera celeste,
nonostante l'ampio giro percorso dal nostro pianeta intorno alla sua stella. Quando,
finalmente, la strumentazione osservativa divenne adeguata, gli astronomi
poterono applicare il metodo della parallasse al calcolo delle distanze
stellari. Nei libri solitamente si riporta che il vincitore di questa
faticosa lotta contro la parallasse fu Friedrich Wilhelm Bessel (1784-1846), matematico e astronomo
tedesco che, nel 1838, pubblicò la prima parallasse stellare riferita alla
stella 61 Cygni. In realtà, quello di Bessel non fu
un tentativo isolato. Anche altri due eccellenti astronomi erano in quegli
stessi anni impegnati in analoghi tentativi. Un altro tedesco, Friedrich Wilhelm Struve
(1793-1864), era alle prese con la parallasse di Vega, mentre lo scozzese Thomas James Henderson (1798-1844)
si stava occupando di Alfa Centauri. La scelta delle stelle era tutt'altro
che casuale: intelligentemente i tre astronomi avevano scelto quelle che
presentavano il più elevato moto proprio, dunque erano con molta probabilità
le più vicine al nostro pianeta. Probabilmente, il primo a giungere a un
risultato concreto fu Henderson, ma i dubbi sull'accuratezza degli strumenti
impiegati lo trattennero dal pubblicare subito il suo lavoro. Fu dunque
Bessel ad annunciare per primo, nel 1838, la misurazione di una parallasse
stellare: il valore da lui ottenuto per 61 Cygni fu
di 0,3136 arcosecondi. Di fronte a un simile valore non si fatica davvero a comprendere come mai gli astronomi abbiano dovuto attendere così tanto tempo prima di vincere la loro battaglia con le distanze stellari. Finalmente quei puntini luminosi osservati fin dall'antichità potevano essere collocati alla giusta distanza: un traguardo che non solo permetteva di cominciare a misurare le dimensioni del cosmo spazzando via secoli di valutazioni assolutamente inaffidabili, ma che dava anche modo agli astronomi di indagare più a fondo sulle grandezze fisiche delle stelle. Nota la loro distanza, infatti, anche i discorsi sulla luminosità e sulle altre grandezze fisiche in gioco potevano insomma avere un corretto fondamento fisico. |