|
|
|
|
|
|
|
|
|
La distanza delle stelle
Claudio
Elidoro
|
Dedichiamo
ancora un po’ d’attenzione all’importante idea della parallasse stellare
provando ad affrontare alcuni quesiti. Per rispetto a Friedrich Bessel, il
primo semplice nodo che proviamo a sciogliere è quello di ripercorrere i suoi
calcoli. Come si è appena ricordato, quando annunciò la parallasse
di 61 Cygni Bessel indicò un valore di 0,3136 arcsec, valore dal quale possiamo giungere, in modo
semplice e rapido, alla distanza della stella espressa in parsec (pc): d = 1 /
0,3136 = 3,18 pc Ma quanto varrebbe tale distanza se, anziché utilizzare
il parsec, volessimo esprimerla in anni luce (a.l.)? In altre parole: quanti
anni luce ci vogliono per fare un parsec? Per effettuare una simile trasformazione è necessario
anzitutto calcolare a quanti chilometri corrisponde un a.l. Per questo ce la
caviamo abbastanza agevolmente. Infatti, arrotondando la velocità della luce
a 300.000 km/s, otteniamo : 1 a.l. = c (velocità della luce) x
1 anno = = 3
x 105 km/s x
(60 x 60 x 24 x
365,25) s = 9,47 x 1012 km D’altra parte, la definizione di parsec impone che: 1 pc = 1 ua / tg (1 arcsec)
= 150 x
106 / 4,84 x 10-6 = 3,09 x 1013 km calcolo
nel quale, vista l’estrema piccolezza dell’angolo, abbiamo considerato il valore
della tangente praticamente identico al valore dell’arco corrispondente (pari
a 4,84 x 10-6 radianti) e abbiamo, per comodità,
considerato l’unità astronomica (ua) pari a 150 milioni di chilometri. I valori trovati ci permettono di calcolare che 1 pc = 3,09 x
1013 / 9,47 x 1012 = 3,26 a.l. Secondo le rilevazioni e i calcoli di Bessel, dunque, 61 Cygni si trova alla distanza di 10,37 a.l. Misure più
recenti della parallasse hanno limato un po’ il valore del 1838, portandolo
agli attuali 0,294 arcsec, con il risultato di
allontanare leggermente 61 Cygni, fino a 11,08 a.l. Un secondo rapido calcolo lo dedichiamo alla valutazione
della distanza limite per la quale il metodo della parallasse possa essere
considerato applicabile (e dunque affidabile). Potremmo essere indotti a ritenere che la rilevazione e
la misurazione di angoli sempre più piccoli possa ritenersi una questione
esclusivamente strumentale. Niente di più sbagliato. Guai, infatti, a
dimenticarci dei pesanti influssi sulle osservazioni astronomiche imposti
dalla nostra atmosfera. La turbolenza atmosferica – e questo lo ha certamente
notato anche chi solo occasionalmente ha provato a dare un’occhiata
nell’oculare di un telescopio – pone un drastico limite alla misurazione di
angoli inferiori al centesimo di arcosecondo. Questo significa che una distanza pari a d = 1 / 0,01 = 100 pc costituisce
praticamente un limite invalicabile per la rilevazione di una parallasse da
Terra. Le cose migliorano enormemente non appena riusciamo a
liberarci dei limiti imposti dall’atmosfera. Lo provano in modo schiacciante
le misurazioni ottenute dal satellite Hipparcos
(acronimo per High Precision Parallax
Collecting Satellite) nel corso della sua
missione (svolta tra il 1989 e il 1993), nella quale raccolse la parallasse
di quasi 120 mila stelle con una precisione di 0,001 arcosecondi
(catalogo Hipparcos) e oltre un milione con
precisione di 0,02-0,03 arcosecondi (catalogo Tycho). Resta comunque il problema della misura della distanza
per le stelle che risultano irraggiungibili con il metodo della parallasse.
Mentre riflettiamo se è il caso di dedicare anche a questo argomento – o a
una parte di esso – una prossima spigolatura, anticipiamo, in una sorta di
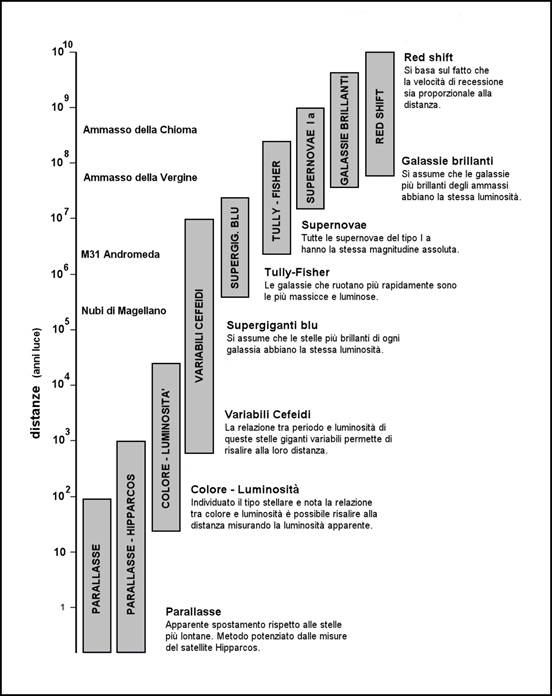
trailer cinematografico, un grafico di facile lettura (Fig. 2) che illustra alcuni dei
possibili metodi a disposizione degli astronomi per spingere sempre più in là
la determinazione delle distanze cosmiche.
Fig. 2. Portata di alcuni
tra i principali metodi a disposizione degli astronomi per misurare le
distanze cosmiche. Come si può notare, si tratta di una vera e propria
“scala” delle distanze, in cui ogni gradino è indispensabile per calibrare
quello successivo. |