|
|
|
|
|
|
|
|
|
Tante stelle, tante storie
Claudio
Elidoro
|
Dato che poco fa abbiamo ribadito che
le stelle più massicce e luminose sono quelle che rimangono meno di tutte sulla
sequenza principale, è doveroso giustificare subito un simile comportamento.
Abbiamo più volte affermato che la sequenza principale è il luogo più
tranquillo del diagramma h-r. Vi
appartengono le stelle che hanno raggiunto il delicato equilibrio tra la
spinta gravitazionale, che tenderebbe a farle collassare, e la spinta verso
l’esterno, esercitata dall’energia termica delle reazioni nucleari. Un simile
equilibrio si mantiene finché la stella dispone del carburante sufficiente ad
alimentare le reazioni. Sintetizzando al massimo, dunque, il tempo di
permanenza in sequenza principale (t)
è dato dal rapporto tra le scorte (che potremmo in modo sbrigativo
identificare con la massa M della
stella) e il consumo (praticamente la produzione energetica, cioè la
luminosità L della stella). In una
precedente spigolatura (marzo 2005), chiamando in causa gli studi compiuti
nel 1926 da Sir Arthur Stanley Eddington, avevamo ricostruito come tutto ciò
comportasse una dipendenza del tipo: t µ
1/M2,5 A voler essere precisi, la relazione
dovrebbe essere molto più complessa, dato che il legame tra la massa e la
luminosità di una stella non è costante. È pur vero che lo si possa esprimere
attraverso un andamento esponenziale del tipo Ma
(con 3 < a
< 4), ma l’esponente a
è in realtà anch’esso una funzione della massa. Quello che a noi importa, comunque, è
evidenziare come mai le stelle più massicce non soltanto siano le più
luminose, ma anche le più prodighe, scialacquando senza criterio le loro
disponibilità energetiche. Un comportamento che trova riscontro nel fatto che
l’estremità superiore della sequenza principale, man mano che trascorre il
tempo dalla nascita di un ammasso stellare, si abbassa sempre di più. Questo
punto, in cui improvvisamente la sequenza principale “piega verso destra”,
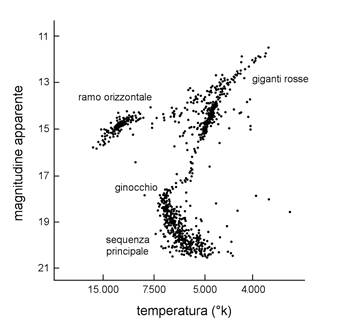
riveste particolare importanza nel caso degli ammassi globulari. Nella Fig. 2 si può osservare il diagramma h-r di m13,
il notissimo ammasso globulare – il più luminoso dell’emisfero boreale –
osservabile nella costellazione di Ercole.
Fig. 2. Diagramma h-r relativo all’ammasso globulare m13. Oltre alla sequenza principale e alla
regione delle giganti, è chiaramente indicato il “ginocchio” o punto di turn-off della sequenza principale. L’importanza del “ginocchio” (o
turn-off) di un ammasso globulare risiede nel fatto che, dalla valutazione
delle età delle stelle che si trovano in quel punto della sequenza
principale, siamo in grado di stimare l’età dell’intero ammasso. Tale
valutazione risulta addirittura meno problematica di quella degli ammassi
aperti e non è solo perché i diagrammi h-r
che li riguardano sono di gran lunga più “popolati” rispetto a quelli degli
ammassi aperti. Quando intendiamo analizzare,
attraverso il suo diagramma h-r,
la popolazione stellare di un ammasso, la premessa irrinunciabile è che tutte
le sue stelle si siano formate pressoché contemporaneamente. Altrettanto
importante, però, è che la popolazione attuale sia anche statisticamente
completa. In altre parole, chi mi garantisce che la popolazione stellare che
osservo ora sia l’evoluzione di quella originale e che una frazione
significativa non si sia dispersa? La densità di un ammasso globulare, però,
è talmente elevata da ostacolarne la disgregazione e questo garantisce che
nessuna stella sia riuscita a sfuggire dal gruppo: popolazione
statisticamente perfetta, dunque. È stata proprio l’analisi dei punti di
turn-off che ha permesso di scoprire che gli ammassi globulari sono
estremamente antichi, di gran lunga più antichi degli ammassi aperti e di
tutte le stelle che si trovano nel disco galattico. Prima di concludere, proviamo a
risolvere un semplice problema riguardante l’età di un ammasso. Immaginiamo
che un ammasso presenti il punto di turn-off in corrispondenza di una
luminosità pari a 81 LSol.
Assumiamo inoltre che, per una stella nei pressi del punto di turn-off, la
relazione massa/luminosità sia del tipo L
= M4. Proviamo con
questi dati a determinare l’età dell’ammasso. Fissando in 10 miliardi di anni la
permanenza del Sole sulla sequenza principale ed esprimendo massa e
luminosità della stella in unità solari abbiamo che: t = 1010 anni [(M/MSol)
/ (L/LSol)] (2) Poiché i dati del problema indicano
che L = 81 LSol, ricaviamo che
A questo punto non dobbiamo far altro
che inserire nella (2) i dati ottenuti, vale a dire: t = 1010
(3/81) ~ 3,7 ´ 108 anni Dal risultato ottenuto, dunque, appare
evidente che l’ammasso su cui stiamo facendo i nostri conti non è sicuramente
un ammasso globulare. Se fosse stato uno di quelli, avremmo trovato un’età
intorno ai 12 miliardi di anni. Una bella differenza! |