|
|
|
|
|
|
|
|
|
Frattali
Annibale
D'Ercole
Osservatorio
Astronomico - Bologna
|
Le forme
della geometria classica sono linee e piani, cerchi e sfere, triangoli e
coni. Esse rappresentano una forte astrazione della realtà, ed Euclide le
utilizzò per costruire una geometria che è durata duemila anni. Fino agli inizi del XX secolo gli astronomi costruirono
su di esse una teoria dell’universo. Ma per la comprensione della complessità
esse risultano essere il tipo di astrazione sbagliato. Le nubi non sono
sfere, le montagne non sono coni. Le linee spezzate ed i grovigli non sono
imperfezioni che distorcono le forme classiche della geometria euclidea. Sono
spesso le chiavi dell’essenza di una cosa. Qual è, ad esempio, l’essenza di
una linea costiera? La sua lunghezza dipende dalle dimensioni del righello
con cui si misura. Se misuriamo la lunghezza di una costa con un righello di
un metro, tutte le anse e le curve più corte verranno trascurate, e il
risultato finale sarà solo un’approssimazione della lunghezza vera.
Intuitivamente, siamo portati a pensare che, utilizzando righelli sempre più
corti, otterremo misure sempre più accurate della lunghezza “vera”. In
verità, con righelli più corti misuriamo un maggior numero di anfratti e
otteniamo valori sempre maggiori della lunghezza. Questo procedimento
converge a un numero finale nel caso si misuri una figura euclidea “liscia”
come, ad esempio, un cerchio. Ma nel caso di una linea costiera la lunghezza
tende all’infinito perché baie e penisole contengono innumerevoli sotto-baie
e sotto-penisole.
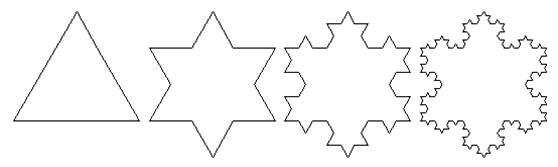
Fig.
1. Fiocco di neve di Koch. Figure
geometriche con questo strano comportamento erano già note ai matematici più
di cento anni fa. Si consideri ad esempio il “fiocco di neve” di von Koch che
si ottiene come segue: si prende un triangolo equilatero e si taglia ogni suo
lato in tre parti; ognuno dei segmenti centrali così ottenuti viene
sostituito con due segmenti uguali a quello eliminato; si ripete l’operazione
per ciascuno dei segmenti presenti e si continua a ripeterla per un numero
infinito di volte. A ogni iterazione, la lunghezza della curva cresce di un
fattore 4/3: se il lato del triangolo di partenza ha lunghezza pari a 1, dopo
il primo passo misura 4/3, dopo il terzo 16/9, dopo il quarto 64/27 e così
via. Questa successione è chiaramente divergente, cioè tende ad assumere un
valore infinito. La straordinarietà del fiocco di neve consiste nel fatto
che, nonostante il suo perimetro sia infinito, la sua area è finita e
certamente inferiore a quella del cerchio che circoscrive il fiocco di neve
contenendolo interamente (ovvero il cerchio che passa per i vertici del
triangolo di partenza). Ma non è tutto: ogni tratto del fiocco di neve, anche
piccolissimo, gode della proprietà dell'autosimilitudine, cioè contiene in sé un’infinita
ricchezza di particolari, di minuscoli triangolini,
ed è quindi anch’esso di lunghezza infinita. Quest’ultima particolarità
implica una proprietà straordinaria della linea che delimita il fiocco di
neve: essa ha una dimensione frazionaria
compresa tra 1 e Le due caratteristiche summenzionate — l’autosimilitudine e l’infinita distanza tra due punti
qualunque sulla curva (se misurata lungo la curva stessa), implicante una
dimensione frazionaria — individuano una curva frattale. Il nome deriva dal latino fractus (spezzato, frantumato)
e, nel 1975, è stato attribuito a questi oggetti geometrici da Benoit
Mandelbrot, il matematico che riprese in anni più recenti lo studio di questi
“mostri matematici” che nel frattempo erano stati parzialmente dimenticati.
Mandelbrot ricevette un sostegno insostituibile dall’avvento dei calcolatori
che permettono di eseguire, in tempi brevi, le numerose iterazioni associate
ai frattali; in ogni caso ebbe l’indubbio merito di capire che i frattali,
lungi dall’essere pure forme matematiche astratte, si ritrovano con una certa
frequenza nella natura che ci circonda. Dalla forma del cervello a quella
delle diramazioni dei dendriti nervosi, dal profilo frastagliato delle foglie
allo schema di sviluppo dei coralli, dalla forma dei fulmini alle linee di
frattura dei materiali da costruzione, dal rumore nei circuiti elettrici
all’andamento temporale del prezzo delle merci, fino ai profili di nubi e
montagne, tutto sembra essere frattale.
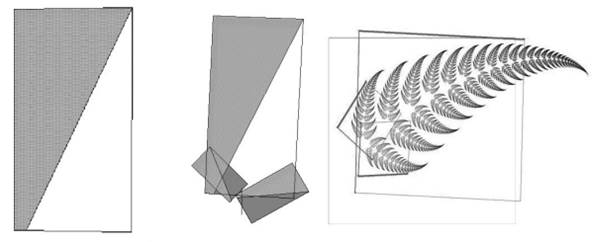
Fig.
2. La felce frattale si ottiene ripetendo un gran numero di volte la
trasformazione mostrata in figura: ogni rettangolo è rimpiazzato da tre
rettangoli più piccoli e uno è ridotto a un segmento, piazzato come mostrato
in figura. Questa ubiquità dei frattali li ha resi utili strumenti
di indagine scientifica (abbiamo ad esempio accennato, in un numero
precedente, alla connessione tra sistemi caotici e frattali) con ricadute
pratiche nei campi più svariati. Ad esempio, la forma complessa di una foglia
di felce può essere descritta compiutamente da un algoritmo simile a quella
del fiocco di neve di Koch (benché più complesso) basato su 24 numeri
soltanto. Viceversa, per rappresentare l’immagine della felce, punto per
punto, con una qualità dell’immagine televisiva, ci vorrebbero centinaia di
migliaia di valori numerici. Questo ci permette di capire come tutta
l’informazione in codice per la formazione di una felce possa essere
contenuta in una spora. Inoltre, questa particolarità è di grande interesse
pratico, perché permette la compressione delle immagini con metodi frattali:
la possibilità di inviare i pochi dati numerici necessari a ricostruire
un’immagine tramite una semplice regola ricorsiva, piuttosto che le
informazioni relative ad ogni pixel dell’immagine stessa, rappresenta un
risparmio di tempo rilevante e l’eliminazione pressoché totale di errori. In
molti film fantasy o di fantascienza la ricostruzione fantastica di fondali o
panorami avviene proprio tramite lo sviluppo di frattali. Si possono creare
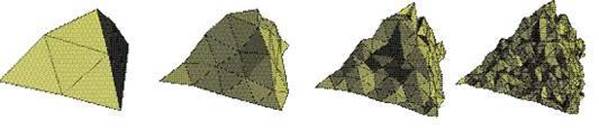
paesaggi frattali con il metodo dello spostamento dei punti medi. I punti
medi dei lati di un triangolo vengono uniti da segmenti e spostati in su o in
giù, fuori dal piano dell’immagine; si ottengono così quattro piccoli
triangoli su cui si ripete il procedimento. L’entità dello spostamento è
casuale e il suo valore massimo, deciso a priori, determina la scabrosità del
terreno frattale.
Fig. 3. Costruzione
di una montagna frattale.
|