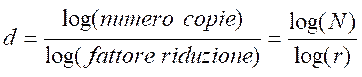Frattali
Annibale D'Ercole
Osservatorio Astronomico - Bologna

Prima di affrontare il concetto di dimensione frazionaria, è bene chiarire cosa si intende quando ci riferiamo alle abituali dimensioni intere a cui siamo abituati. È banale affermare che una linea ha dimensione 1, una superficie ha 2 dimensioni ed un cubo ha 3 dimensioni. Tuttavia, incontriamo un certo imbarazzo se siamo chiamati a dare una definizione più precisa e a specificare meglio la differenza, ad esempio, tra una linea e un piano. Si potrebbe affermare che lungo una linea ci si può muovere solo lungo una direzione, mentre su di un piano ogni movimento è dato dalla combinazione del moto lungo due direzioni indipendenti. In altre parole, il piano è bidimensionale perché è dotato di “altezza” e “larghezza”: non c’è dubbio che questi argomenti appaiano al contempo sensati e tautologici. Un ulteriore elemento di confusione si aggiunge quando consideriamo una linea curva posta su un piano o, più ancora, nello spazio (come una sorta di sottile fil di ferro contorto). In questo caso, nonostante la definizione data precedentemente, siamo portati a considerare la curva un’entità tridimensionale.

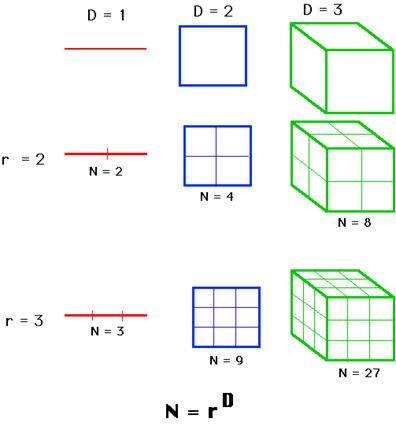
I matematici sono riusciti a dare una definizione di dimensione rigorosa e priva della confusione cui abbiamo accennato. Il prezzo da pagare per questo rigore è l’abbandono dell’intuizione visiva a favore di una formulazione matematica. Un segmento può essere suddiviso, poniamo, in 4 parti tra loro uguali. A parte che per la lunghezza, queste sezioni sono simili al segmento di partenza che, per questo, viene detto essere stato suddiviso in parti autosimili. Ognuna di queste parti, se ingrandita 4 volte, riproduce il segmento di partenza. In generale, se dividiamo il segmento in N parti autosimili, ognuna è dotata di un fattore di riduzione r pari a N.

Consideriamo ora un quadrato e dividiamolo, tramite due linee incrociate, in N= quadrati uguali, ognuno simile al quadrato di partenza ma con il lato ridotto di un fattore r=2. Se dividiamo il quadrato in N= quadrati autosimili, il fattore di riduzione di ognuno di questi quadrati più piccoli è pari a r=. In generale, un quadrato può essere suddiviso in N=r² copie autosimili, ciascuna con un fattore di riduzione pari ad r. Analogamente, un cubo può essere suddiviso in N=r³ cubi più piccoli, ognuno con i lati ridotti di un fattore r. A questo punto abbiamo già capito che la dimensione è data dal numero che appare a esponente del fattore di riduzione e che lega tale fattore al numero di copie autosimili. Sfruttando la proprietà dei logaritmi per cui log(r^d)=dlog(r), la dimensione d è dunque definita come:

.

Pertanto, nel caso del segmento, del quadrato e del cubo otteniamo, rispettivamente,

,

,

.

Fig. 4. Definizione di dimensione.

Come semplice esempio iniziale di oggetto frattale, ovvero con dimensione frazionaria, consideriamo un segmento di lunghezza unitaria, dividiamolo in tre parti uguali di lunghezza 1/3 e sottraiamo l’intervallo intermedio. Applichiamo la stessa procedura ai due segmenti rimanenti, ed otteniamo 4 segmenti di lunghezza 1/9=1/3². 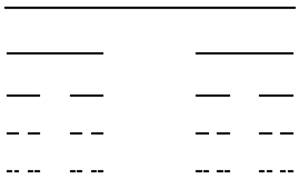Iterando (ossia, ripetendo) questa procedura un infinito numero di volte, otteniamo un insieme di segmenti infinitamente corti noto come polvere di Cantor. Qual’è la dimensione di questo segmento infinitamente “bucherellato”? In questo caso, ad ogni passo il numero di segmenti raddoppia, cioè N=2, e la lunghezza di ogni segmento si riduce a 1/3, ovvero r=3. Dunque, la dimensione è pari a d=log(2)/log(3)=0,63. Abbiamo un oggetto geometrico con dimensione inferiore a 1 ma superiore a 0: un oggetto intermedio tra il punto e la retta.

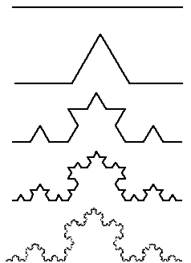
Fig. 5. Polvere di Cantor.

Un esempio un poco più complesso è dato dalla curva di Koch. In questo caso il solito segmento unitario iniziale viene diviso di nuovo in 3 parti di lunghezza pari a 1/3, ma la sezione centrale viene ora sostituita da due segmenti, anch’essi di lunghezza pari a 1/3. Si ripete questa procedura ad ogni lato della figura così ottenuta, e si procede un infinito numero di volte, ottenendo un oggetto infinitamente “frastagliato”. Come nel caso della polvere di Cantor, anche ora ad ogni passo r=3, ma il numero del lati quadruplica, dunque N=4. In conclusione, la dimensione della curva di Koch è pari a d=log(4)/log(3)=1,26: una dimensione intermedia tra la retta e il piano.

Fig. 6. Curva di Koch.

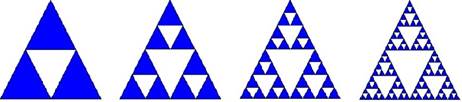
Consideriamo ora una figura geometrica frattale nota come triangolo di Sierpinski. Questa figura si ottiene tramite il seguente processo iterativo. Si parte da un triangolo e si adottano i punti di mezzo di ciascun lato come vertici di un nuovo triangolo centrale che viene sottratto dall’originale. Rimangono così N=3 triangoli simili a quello di partenza, ognuno con un’area pari ad un quarto dell’area originale ed un fattore di riduzione del lato pari a r=. A questo punto ripetiamo il procedimento per ognuno dei tre triangoli, e poi ancora e ancora, ottenendo triangoli autosimili sempre più piccoli. Iterando infinite volte, otteniamo un oggetto certamente più articolato di un segmento, ma più “povero” di una superficie a causa degli infiniti “buchi triangolari” presenti. In effetti, applicando la definizione data più sopra, vediamo che la dimensione di questo triangolo è frazionaria, e compresa tra 1 e 2: più precisamente d=log(3)/log(2)=1,585.

Fig. 7. Triangolo di Sierpinski.

Rappresentazioni bidimensionali di frattali che possono dare luogo ad immagini verosimili si ottengono tramite processi ricorsivi un poco più complessi del tipo:

x_n+1=ax_n+by_n+e,

y_n+1=cx_n+dy_n+f,

dove a, b, c, d, e, f, sono costanti. Fissati i valori delle costanti e delle coordinate iniziali x₀ e y₀, vengono individuati progressivamente dalle due formule coppie di valori (x₁,y₁), (x₂,y₂), …, (x_n,y_n). Colorando diversamente sul piano x-y i punti così ottenuti, si ottengono figure frattali che possono anche rappresentare assai verosimilmente, a seconda della scelta delle costanti e dei punti di partenza, felci, foglie, montagne etc. Frattali più elaborati, quali gli insiemi di Mandelbrot e Julia, si possono ottenere tramite algoritmi ricorsivi non lineari e nel campo dei numeri complessi.

Fig. 8. Insieme di Mandelbrot.

Fig. 9. Insieme di Julia.

---

Home Spigolature

Livello Base