|
All’interno di una cabina di
ascensore ferma e sospesa nel campo gravitazionale della Terra, un
osservatore percepisce tale campo tramite la pressione esercitata dal
pavimento sulla pianta dei suoi piedi per controbilanciare il suo peso.
Se l’osservatore lascia andare un qualunque oggetto che tiene in mano, tale
oggetto cade sul pavimento. Se il sostegno della cabina viene reciso,
l’ascensore cade verso il basso a velocità crescenti. Tuttavia la sua accelerazione
- ovvero il tasso di variazione di velocità nell’unità di tempo – è costante.
Questa è una proprietà del
campo gravitazionale nei pressi della superficie terrestre nota fin dai tempi
di Galileo: tutti gli oggetti, lasciati a sé stessi, cadono verso terra con
una accelerazione costante che è uguale per tutti, indipendentemente dalla
loro massa.
Einstein si rese conto che, in assenza di un campo gravitazionale esterno,
questo comportamento poteva essere simulato da un sistema di riferimento
accelerato.
Immaginiamo, infatti, che la nostra cabina sia posta in una zona di universo
lontana da grandi concentrazioni di massa, e dunque priva di un campo
gravitazionale apprezzabile. Supponiamo inoltre che, tramite un razzo,
la cabina venga agganciata al soffitto e trascinata verso "l’alto"
con accelerazione costante. L’occupante percepirà la pressione
del pavimento contro i suoi piedi, analogamente alla pressione esercitata
contro la nostra schiena dal sedile quando ci troviamo all’interno di
un’automobile in fase di accelerazione. Se poi l’occupante lascia
andare un oggetto che tiene in mano, tale oggetto tende a rimanere fermo
(perché nessuna forza agisce su di lui); tuttavia il pavimento gli va
incontro con moto accelerato, e all’osservatore nella cabina sembrerà che
l’oggetto cada verso il pavimento. A tutti gli effetti le cose
nella cabina vanno come se l’ascensore fosse fermo all’interno di un campo
gravitazionale reale.
Questa indistinguibilità tra un sistema di riferimento accelerato ed uno
fermo e sottoposto a forza di gravità esterna è stata battezzata da Einstein Principio
di Equivalenza.
Queste considerazioni sono
talmente semplici da apparire banali. Eppure Einstein riuscì a pervenire,
proprio tramite queste apparenti banalità, a conclusioni stupefacenti
riguardo alla natura della gravità ed alla sua influenza sulle proprietà
dello spazio e del tempo. Einstein formulò il Principio di
Equivalenza nel 1907, due anni dopo aver pubblicato la Teoria della
Relatività ristretta in cui mostrava che spazio e tempo sono percepiti
diversamente da osservatori che si muovano l’uno rispetto all’altro.
Gli ci vollero però altri otto anni di sforzi enormi prima che le sue
intuizioni riguardo alla gravità potessero concretizzarsi in una teoria
coerente. Questa Teoria della Relatività generale ha trovato da allora
numerose conferme sperimentali e rappresenta attualmente la migliore teoria
per descrivere i campi gravitazionali.
Noi qui ripercorreremo
l’intuizione di partenza di Einstein che lo ha portato a concludere che, in
presenza di un campo gravitazionale, spazio e tempo si deformano. Per fare
questo abbandoniamo l’esempio dell’ascensore, in cui la velocità varia di
intensità ma non di direzione, e consideriamo un moto accelerato particolare,
quello in cui il valore della velocità non cambia, ma cambia la direzione del
moto.
|
|
|
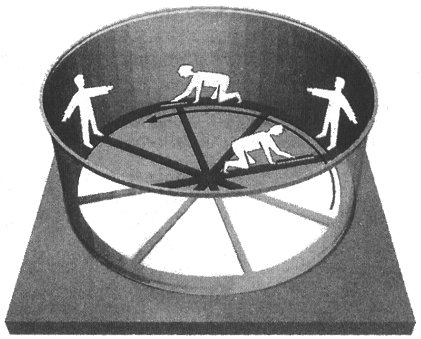
Figura 1 - Il Rotor
|
Questa è proprio il tipo di
accelerazione avvertito da un osservatore posto su una giostra. In
particolare, si consideri il Rotor che si trova nei
parchi di divertimento (Fig. 1). Si tratta di un cilindro in veloce rotazione
i cui occupanti, appoggiati alla parete interna, si sentono pressati contro
tale parete a causa della forza centrifuga.
Un’attenta calibrazione della velocità di rotazione può indurre
nell’osservatore la sensazione di essere "sdraiato" in terra; ed
infatti i progetti delle stazioni spaziali prevedono di riprodurre in questo
modo una gravità artificiale nello spazio.
Sembra che proprio con questo esempio Einstein abbia intuito che la gravità
deforma lo spazio e il tempo.
Lo scienziato tedesco, in effetti, aveva già dimostrato con la sua Teoria
della Relatività ristretta che spazio e tempo sono misurati diversamente da
due osservatori in moto relativo uniforme (ossia non accelerato) l’uno
rispetto all’altro. Abbiamo illustrato in questa rubrica (n. 1/2000)
come l’orologio di un viaggiatore posto su un treno appare scorrere più
lentamente ad un osservatore posizionato in terra, accanto ai binari.
Ed abbiamo anche mostrato che un righello posto sul treno parallelamente ai
binari sembra essere più corto all’osservatore esterno, mentre un righello
posto ortogonalmente alla direzione del moto mantiene inalterata la sua
lunghezza sia per questo osservatore che per il viaggiatore.
Adattiamo ora questa esperienza al caso del Rotor, considerando un osservatore posto al suo interno
(l’analogo del viaggiatore sul treno) ed un osservatore stazionario posto
all’esterno (l’analogo dell’osservatore accanto ai binari). L’osservatore
interno misura la circonferenza della giostra tramite un righello posto
ripetutamente lungo il perimetro della base; successivamente, con la stessa
tecnica, l’osservatore misura il raggio della giostra ritrovando, nel caso il
Rotor sia fermo, il classico risultato della
geometria euclidea, ossia che il rapporto tra la circonferenza ed il raggio
di un cerchio vale 2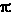 . Questo
risultato vale, naturalmente, anche per l'osservatore esterno.
Se però le stesse operazioni di misura vengono
eseguite con il Rotor in movimento, il risultato è
diverso. La lunghezza del raggio effettivamente è la stessa del caso statico
perché il righello viene posto ortogonalmente al moto durante questa misura,
e non si verifica nessuna contrazione relativistica. Tuttavia, durante la
misura della circonferenza, il righello è posto nella direzione del moto e si
contrae; se il righello è più corto, la circonferenza lo contiene un numero
maggiore di volte ed il rapporto tra circonferenza e raggio risulta maggiore
di 2.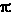
Ora, l’occupante chiuso nel Rotor non può osservare l’esterno e dunque ignora
di trovarsi su un sistema rotante; egli crede di trovarsi in un riferimento
fisso, ed attribuisce la forza che lo spinge verso le pareti alla forza di
gravità generata da una qualche distribuzione esterna di massa. Pertanto,
per questo osservatore, il singolare risultato geometrico deve dipendere
dalla presenza della gravità ed implica una distorsione dello spazio.
|
|
|
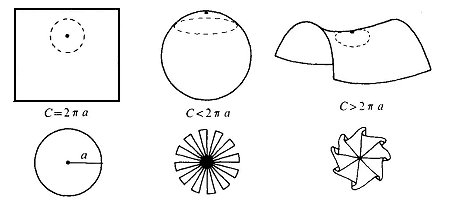
Figura 2
|
Nella Figura 2 sono mostrati
tre cerchi di identico raggio ma di circonferenza diversa. Questa diversità
dipende dal tipo di superficie su cui i cerchi sono tracciati.
Il rapporto 2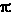 tra circonferenza e raggio si ritrova
per il cerchio sulla superficie piana; nel caso della superficie curva
sferica il rapporto è minore, mentre è maggiore per la superficie curva
"a sella".
Questo semplice esempio bidimensionale è estensibile allo spazio
tridimensionale ed ha indotto Einstein ad ipotizzare che le relazioni
spaziali della geometria piana (la familiare geometria euclidea) non sono
valide per un osservatore in moto accelerato.
Ma, per il Principio di Equivalenza, questo vuol dire che la geometria
euclidea smette di essere valida anche in presenza di un campo gravitazionale
reale.
Ma in un riferimento
accelerato anche il tempo viene distorto. La Teoria della Relatività
ristretta ci dice che l’orologio del viaggiatore sul treno scandisce il tempo
tanto più lentamente rispetto all’orologio dell’osservatore accanto ai binari
quanto maggiore è la velocità del treno. Analogamente, il tempo per
l’occupante del Rotor scorre più lentamente
rispetto all’osservatore esterno. Tanto più l’occupante si allontana
dal centro, tanto maggiore è lo spazio percorso per completare un giro;
quindi la sua velocità aumenta con la distanza dal centro, e il suo orologio
ritarda sempre più. Dal momento che anche la forza centrifuga aumenta
con la distanza dal centro, l’osservatore all’interno del Rotor
conclude che il tempo scorre tanto più lentamente quanto più intenso è il
campo gravitazionale.
Di nuovo, per il principio di equivalenza, il tempo deve scorrere più
lentamente anche in un campo gravitazionale reale.
|
