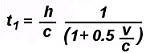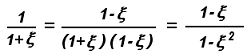Se si assume che il Principio di Equivalenza è vero,
allora si può dedurre che la gravità opera una distorsione sia spaziale che
temporale. Quest’ultima è più semplice
da ricavare, ed in effetti fu la prima di cui Einstein si accorse.
Consideriamo la cabina di un ascensore posta in una
regione priva di un’apprezzabile forza di
gravità, e supponiamo che sia trascinata verso "l’alto", ovvero in direzione del
soffitto, con accelerazione uniforme g tramite un
missile. Un dispositivo temporale posizionato sul soffitto invia un
impulso luminoso al secondo verso il pavimento.
Un osservatore posto sul pavimento riceve questi impulsi,
ma nota che si susseguono ad intervalli minori di un secondo; questo accade
perché il pavimento si muove verso questi impulsi intercettandoli un poco
prima. Pertanto all’osservatore
sul pavimento l’orologio posto sul soffitto
apparirà procedere un poco più in fretta.
D’altra
parte questo osservatore non ha modo di guardare fuori della cabina, e
ritiene che la pressione da lui esercitata sul pavimento sia dovuta ad un
campo gravitazionale esterno, ed attribuirà a quest’ultimo
l’accelerazione dell’orologio
sul soffitto.
Per il Principio di Equivalenza, allora, anche un campo di
gravità reale deve influenzare lo scorrere del tempo allo stesso modo.
Deduciamo ora
quantitativamente la distorsione dello scorrere del tempo nell’assunzione che le velocità v
raggiunte dalla cabina siano molto minori della velocità della luce c.
E' noto che un oggetto
che si muove con accelerazione costante g acquista, dopo un
tempo t, una velocità v=gt
percorrendo uno spazio x=0.5gt2.
Dunque, le posizioni del
pavimento e del soffitto della cabina al tempo t sono date
da
dove h è l’altezza della cabina.
Supponiamo ora che dal
soffitto partano due impulsi luminosi: il primo è emesso al tempo t=0
e ricevuto al tempo t1, mentre il secondo è emesso
al tempo t= 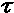 e ricevuto al tempo t1+
e ricevuto al tempo t1+ t (in fisica classica t (in fisica classica  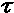 = = t, ma questo non è più vero nella
Teoria della Relatività, come vedremo tra poco). t, ma questo non è più vero nella
Teoria della Relatività, come vedremo tra poco).
La distanza percorsa dal
primo impulso è: xs
( 0 ) - xp ( t1 ) = ct1.
Quella percorsa dal
secondo impulso è minore ed è:
xs ( 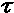 )
- xp (t1+ )
- xp (t1+ t) = c (t1 + t) = c (t1 +  t - t -  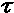 ). ).
Tenendo conto delle
equazioni (1a) - (1b) si ottiene
In definitiva si ottiene
Operando una sottrazione tra queste due equazioni si
ricava
Ora, ricordando che v = gt , l’equazione (2a) può essere riscritta come
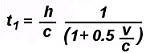
ovvero, avendo assunto v
/ c <<1 ,
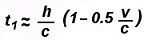
Quest’ultimo passaggio è stato ottenuto dalla
seguente catena di uguaglianze:
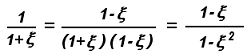
Se 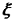 è più piccolo di 1, ancor più lo
sarà è più piccolo di 1, ancor più lo
sarà 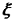 2 che può dunque essere trascurato. 2 che può dunque essere trascurato.
Questo ci porta ad ottenere 1/(1+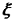 )~(1- )~(1-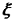 ). ).
Dopo aver sostituito questa
espressione di t1 nell’equazione (3), si ottiene
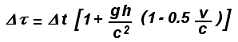
Finalmente, trascurando una
volta ancora il termine 0.5 v/c <<1, si ottiene l’espressione finale
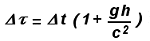
In assenza di accelerazione i
due intervalli di tempo sono uguali; l’accelerazione,
invece, produce un rallentamento dell’orologio
sul pavimento rispetto a quello sul soffitto.
L’osservatore all’interno
della cabina, inconsapevole di viaggiare "a rimorchio" di un razzo,
attribuisce tale rallentamento all’azione del
campo gravitazionale esterno a cui crede di essere assoggettato.
Per il Principio di
Equivalenza un campo di gravità reale deve produrre gli stessi effetti: un
orologio posto alla superficie di un pianeta marcia più lentamente di uno
posto in quota.
Effettivamente questa
affermazione è stata verificata sperimentalmente sulla Terra nel 1960 dai due
fisici Pound e Rebka sfruttando proprio l’espressione per  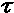 ottenuta più sopra. ottenuta più sopra.
Ricordiamo che questa
formula approssimata è valida nel caso di campi gravitazionali deboli (la cui
accelerazione, cioè, produce velocità assai inferiori a quella della luce) e
uniformi; ed in effetti la gravità della Terra non provoca alte velocità di
caduta e può essere assunta costante se non ci si allontana eccessivamente
dalla superficie.
|