|
|
|
|
|
|
|
|
|
La radiazione Cherenkov
Claudio
Elidoro
|
La possibilità che la velocità della
luce venga in qualche modo “rallentata” in un dielettrico è la chiave che ci ha
permesso di introdurre e spiegare la radiazione Cherenkov.
Questa caratteristica, tipica di ogni materiale, è descritta, dal punto di
vista fisico, dall'indice di rifrazione n. Si noti che non si tratta di un valore costante, ma di
una grandezza che è funzione della lunghezza d'onda, dunque sarà un n(λ). Per uno specifico
materiale, dunque, la luce è caratterizzata da una velocità cm data da: cm = c / n(λ) Si è detto che la condizione
affinché si possa assistere a emissione di radiazione Cherenkov
è che la velocità della particella carica (vp) sia
almeno uguale alla velocità della luce in quel mezzo. Si dovrà cioè avere c / n(λ) ≤ vp < c, condizione che, nel caso dell'acqua citato
in precedenza (per la quale n ≈
1,33), diventa 0,75 c ≤ vp < c. Proviamo ora a esaminare
più da vicino la situazione della particella carica che si sta muovendo nel dielettrico
con una velocità idonea a produrre radiazione Cherenkov
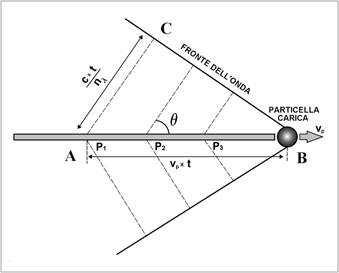
e valutiamo ciò che accade aiutandoci con la Fig. 2. Mentre la particella
carica si muove con velocità vp
dal punto A al punto B,
passando progressivamente per i punti intermedi P1, P2 e P3, la radiazione prodotta si diffonde
percorrendo un tratto che, per il punto A, è pari a (c ·
t) / n(λ). La condizione affinché la radiazione
prodotta nei vari istanti interferisca in modo costruttivo (cioè le onde non
si annullino vicendevolmente) è che sia in fase e si venga a formare un
fronte d'onda (BC nella figura).
Fig. 2. Affinché si crei il fronte d'onda
e dunque la radiazione diventi rilevabile, è necessario che le onde
provenienti dai vari punti della traiettoria siano in fase. Questo impone un
preciso valore per l'angolo θ. Si noti che l'inviluppo del fronte d'onda
sarà una superficie conica la cui apertura è strettamente legata a θ. Esiste dunque un angolo θ
ben preciso, legato al dielettrico e alla velocità della particella, sotto il
quale quel fronte d'onda potrà essere osservato come radiazione. Semplici
considerazioni geometriche, infatti, ci suggeriscono che: cos θ = AC / AB = (c · t / n) / vp · t = (c / vp) / n. Questo fronte d'onda
costituisce un inviluppo conico di apertura ben definita (legata al valore di
θ) e vertice coincidente con la particella in moto, una
situazione che riproduce in modo fedele il “cono di Mach” che si incontra nella trattazione del bang sonico. Un'ultima rapida
considerazione riguarda il colore tipico della radiazione Cherenkov.
Premesso che la radiazione prodotta ha uno spettro continuo, i manuali di
elettromagnetismo riportano che il numero di fotoni prodotti (Nph)
da questo fenomeno è definito da una relazione piuttosto complessa che noi,
per comodità, possiamo sintetizzare in Nph µ 1 / λ2. Immediato notare come l'emissione
risulti più pronunciata man mano ci si sposta verso lunghezze d'onda più
piccole. Ecco spiegato come mai, nella sua componente visibile, la radiazione
Cherenkov sia caratterizzata da un predominante
colore blu. |