|
|
|
|
|
|
|
|
|
La distanza del Sole
Claudio
Elidoro
|
Dopo aver
affrontato in una precedente Spigolatura (GdA, vol.
35, n. 2 – giugno 2009) il problema della distanza del nostro satellite,
proviamo a ripercorrere il lungo cammino e le differenti tecniche che hanno
portato gli astronomi a calcolare la distanza che separa la Terra dal Sole
giungendo in tal modo a definire l’unità chiave delle distanze astronomiche.
In quell’occasione avevamo esaminato le osservazioni e le valutazioni che,
due secoli e mezzo prima di Cristo, condussero Aristarco (iv-iii sec. a.C.) a una corretta valutazione della
distanza lunare. Non apparirà poi così strano, dunque, che il nostro cammino
riprenda proprio dal grande astronomo di Samo. L'idea
di misurare quanto distante fosse il Sole, almeno in linea di principio, era estremamente
semplice. Poiché le fasi lunari sono il frutto del variare della condizione
di illuminazione del nostro satellite da parte del Sole, una Luna illuminata
esattamente a metà è il segno che la congiungente Luna-Sole è perfettamente
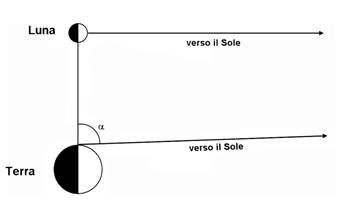
perpendicolare alla congiungente Luna-Terra (la Fig. 1 riuscirà a convincere coloro che fossero ancora
dubbiosi).
Fig. 1. Se del triangolo
rettangolo costruito quando la Luna è al primo o all'ultimo quarto riusciamo
a misurare l'angolo a, ci sarà possibile determinare
anche il lato che più ci interessa, vale a dire la congiungente Terra-Sole. Con
un ragionamento corretto, Aristarco riteneva che la misurazione dell'angolo
Luna-Terra-Sole (angolo a nella figura) avrebbe permesso di
risolvere il triangolo rettangolo e, conseguentemente, le proporzioni tra i
suoi lati. Questo comportava che, conoscendo un suo lato – la distanza della
Luna – fosse possibile risalire anche alla distanza del Sole dalla Terra. Il
guaio è che una simile misurazione è incredibilmente delicata, praticamente
impossibile per Aristarco con gli strumenti di cui poteva disporre. Il greco,
infatti, valutò quell'angolo di 87°, un valore davvero molto vicino alla
misura nota ai nostri giorni (89° 51'). Purtroppo, però, questa che ci appare
come una piccola differenza ha un peso enorme negli sviluppi del calcolo.
Aristarco, infatti, giunse a stabilire che il Sole fosse solo 19 volte più
distante della Luna (dunque circa 7.200.000 km) e non le 389 volte che si
possono ottenere con il valore corretto. Questo bastò, comunque, al grande
astronomo per comprendere come il Sole fosse più grande della Terra,
portandolo quindi a ipotizzare che fosse quello, e non la Terra, al centro
dell'universo. Rimaniamo
ancora un momento nell'antichità classica per segnalare quanto Eusebio di
Cesarea (ii-iii sec. d.C.)
riferisce di Eratostene (iii-ii
sec a.C.) e della sua valutazione della distanza del Sole, stimata in «stadiwn muriadaV tetrakosiaV kai oktwkismuriaV» (letteralmente: “400 miriadi di stadi
e 80000”). Frase un po' sibillina, tanto che sono state proposte due
traduzioni davvero molto distanti tra loro: la prima (Edwin Hamilton Gifford, 1903) propone 4.080.000 stadi, mentre l'altra
(Edouard del Places, 1974-1991) propone 804.000.000 stadi. Utilizzando il
valore dello stadio greco (tra i 185 e i 190 metri), le due traduzioni
conducono a un valore di circa 765.000 chilometri la prima e a circa 150
milioni di chilometri la seconda. Stando a quest'ultima interpretazione,
dunque, Eratostene avrebbe determinato la distanza Terra-Sole con un errore
solamente del 2%. Aspettiamo, però, a gridare al prodigio: forse è il caso di
lasciare che gli esperti della Grecia classica giungano a una interpretazione
meno incerta delle parole di Eusebio. Prima
che gli astronomi si occupassero nuovamente della distanza Terra-Sole si
dovette attendere la disponibilità di nuovi strumenti osservativi e,
soprattutto, di quei potenti strumenti teorici costituiti dalle leggi di
Keplero; in particolar modo la terza, che lega tra loro in modo semplice e
preciso le distanze e i periodi di rivoluzione degli oggetti della famiglia
del Sole. Riuscendo dunque a misurare la distanza di un qualunque pianeta dal
Sole si sarebbe potuti risalire anche alla distanza che separa la Terra dalla
sua stella. Nel
1672, approfittando di una favorevole opposizione di Marte, Gian Domenico
Cassini e Jean Richer misurarono dalla Francia e
dalla Cayenne la parallasse del pianeta e riuscirono in tal modo a
determinare che la distanza del Sole fosse di circa 142 milioni di
chilometri. Pian piano, dunque, ci si stava avvicinando al valore corretto. Verso
la fine del xvii secolo,
riprendendo le proposte di Jeremiah Horrocks e
James Gregory, Edmond Halley suggerì che un miglior risultato sarebbe giunto dalle
osservazioni del transito di Venere sul disco solare, un metodo che venne
provato nel 1761, nel 1769 e poi ancora nel 1874 e nel 1882 (vedi GdA, vol. 29, n. 4 – dicembre 2003). Una recentissima
applicazione di questo metodo, con risultati davvero lusinghieri, la si è
avuta nella campagna internazionale condotta durante il transito del 2004 da
oltre 2700 gruppi di osservatori da ogni parte del mondo, un migliaio dei
quali erano gruppi scolastici. Prima
che l'avvento delle misurazioni radar prendesse il sopravvento quale metodo
più affidabile e preciso per giungere alla determinazione della distanza
Terra-Sole, è doveroso segnalare l'importante ricaduta sul problema prodotta
dalla scoperta dell'asteroide 433 Eros. Il suo passaggio ravvicinato, nel
1900-1901, venne magistralmente sfruttato da Arthur Hinks
per migliorare notevolmente l'accuratezza della parallasse solare, ma ancora
meglio fece Harold Spencer Jones in occasione del passaggio del 1930-1931. Il
suo valore della parallasse solare (8,79 secondi d’arco) venne considerato
definitivo fino al 1968. Attualmente
la determinazione della distanza del Sole viene effettuata ricorrendo a
misure radar o alla telemetria delle sonde spaziali, in grado di fornire le
posizioni dei pianeti interni con estrema precisione. Prima
di approfondire la nostra indagine intorno alla distanza Terra-Sole è
opportuna un'importante precisazione. È vero che tale distanza viene
frequentemente indicata con il termine di unità astronomica (au, secondo
lo standard raccomandato dall'Unione Astronomica Internazionale) e
normalmente le due cose vengono considerate quasi come sinonimi, ma non è
proprio così. In effetti, originariamente l'au era stata definita come la
lunghezza del semiasse maggiore dell'orbita terrestre, ma nel 1964, in
occasione dell'Assemblea generale tenutasi ad Amburgo, l'Unione Astronomica
Internazionale (iau)
raccomandò che da lì in poi l'au avrebbe dovuto essere esattamente pari a
149.600.000 chilometri. In pratica veniva stabilito che essa diventasse una
sorta di costante sulla quale eventualmente calibrare le altre grandezze (per
esempio la parallasse solare o il rapporto di massa tra il Sole e il sistema
Terra-Luna). Dodici anni più tardi, però, l'Assemblea generale iau di
Grenoble sancì un'importante svolta. In tale circostanza, infatti, l'au venne
definita come la distanza tra il centro del Sole e una particella di massa
trascurabile posta in orbita circolare intorno al Sole il cui periodo era
esattamente di 365,2568983 giorni. Dal 1976, dunque, una au misura esattamente
149.597.870,691 km, valore ritoccato a 149.597.870,700 km nel 2009, per
adeguarsi alle ultime misurazioni. |