|
|
|
|
|
|
|
|
|
La distanza del Sole
Claudio
Elidoro
|
Abbiamo accennato alla terza legge di
Keplero; doveroso quindi chiarire il suo ruolo nella determinazione della distanza
del Sole. La legge afferma che per ogni oggetto orbitante intorno al Sole il
quadrato del suo periodo (P) è proporzionale al cubo del semiasse maggiore
(a) della sua orbita. Per tutti i pianeti,
dunque, sarà P2
/ a3 = costante Poiché tale costante di
proporzionalità è identica per tutti i pianeti, avremo che P2Venere
/ a3Venere = P2Terra / a3Terra Se in questa relazione
esprimiamo i periodi orbitali (che conosciamo bene) e i semiassi orbitali
usando come unità di misura i valori della Terra, otteniamo che aVenere = 0,723 aTerra relazione che mi permette, una volta
conosciuto aVenere, di risalire alla
misura di aTerra. Le osservazioni del
transito permettono di determinare la distanza tra Venere e la Terra, ma da
questa è possibile ottenere la distanza Venere-Sole e da lì aTerra. Proviamo ora a esaminare
più da vicino il metodo del transito di Venere così caro ad Halley. Almeno un
paio di motivi ci inducono a farlo. Il primo è che in occasione del transito
del 2004 il lavoro osservativo svolto dai partecipanti alla campagna
internazionale (molti dei quali non professionisti) ha portato a un valore di
149.608.708 km ± 11.835 km, solamente lo 0,007% più grande di quello
"ufficiale" ottenuto grazie a misure radar. Un incredibile successo
che sottolinea la bontà del metodo. Il secondo motivo è che tra un paio
d'anni (il 6 giugno 2012) ci sarà un nuovo transito, ghiotta occasione per
una nuova campagna osservativa. Purtroppo, in Italia potremo gustarne
solamente la parte conclusiva, ma potrebbe essere un ottimo spunto per le
scuole e i gruppi di astrofili per una interessante esperienza (notizie e
proposte di attività si possono reperire sul sito ufficiale
www.transitofvenus.org). Vediamo dunque più da
vicino il ragionamento di Halley. Esagerando la situazione, la Fig. 2 mostra la geometria della
situazione osservativa del transito di Venere.
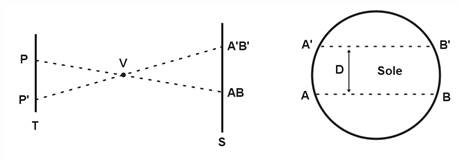
Fig. 2. Schematizzazione (non in scala) della geometria riguardante
l’osservazione del transito di Venere. Un osservatore in P
vedrà il pianeta attraversare il Sole lungo il tragitto AB, mentre un altro
osservatore posto in P' vedrà il tragitto A'B'. Conoscendo la distanza PP',
dunque, basterebbe misurare l’angolo che separa i due percorsi e sfruttare la
trigonometria per determinare la distanza di Venere e quella del Sole. Purtroppo, nella realtà
i due percorsi sono estremamente vicini l’uno all’altro, dunque la determinazione
della loro separazione D non è così semplice. Ciò che Halley e gli
altri avevano notato, però, era che si poteva giungere allo stesso risultato
attraverso la misurazione delle durate dei transiti (il moto di Venere,
infatti, è praticamente identico da qualsivoglia località sulla Terra lo si
osservi). Seguiamo il ragionamento di Halley utilizzando la Fig. 3 come riferimento. Per non
complicarci troppo la vita, considereremo Venere puntiforme; dunque, nelle
formule incontreremo solamente R (raggio apparente del Sole) anzichè (R - r) cioè la differenza tra questo e il raggio
di Venere.
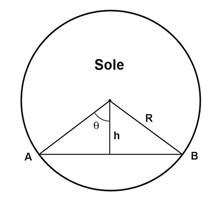
Fig. 3. Dalla figura ricaviamo
che h = R cosq Un altro osservatore rileverà
un transito più lungo, dunque l’angolo sarà leggermente maggiore. Pertanto: h' = R cos(q + d) Applicando alcuni
passaggi trigonometrici e, vista la sua esiguità, approssimando cosd a
1 si ricava che h'
= R (cosq – sinq sind) da cui D = h – h' = R sinq sind (1) Se indichiamo con T e T'
i tempi di transito, proporzionali ovviamente ai due percorsi del pianeta
sullo sfondo del Sole (k indica tale proporzionalità), avremo che: T = 2k R sinq e T' = 2k sin(q + d) Quello che ci interessa
è la valutazione del rapporto DT/T che, dopo aver svolto alcuni
passaggi trigonometrici, risulta essere DT/T
= cosq sind /sinq da cui sind = (DT/T)(sinq/cosq) Pertanto la (1) diventa D = (DT/T) (sin2q /
cosq) Relazione che, confermando
l’idea di Halley, mostra come la valutazione dei tempi e la misura
dell’ampiezza dell’angolo q possa condurci alla separazione D. Questo non significa
affatto che si tratta di un procedimento semplice. Infatti, non solo il
valore di D è talmente esiguo da risultare paragonabile alle dimensioni
angolari di Venere, ma vi sono anche altri fattori di complessità che qui
abbiamo tralasciato. Basti segnalare, per esempio, che nella valutazione dei
due percorsi sul Sole si dovrà mettere in conto la sfericità della nostra
stella; dunque, sarà necessario un fattore correttivo. Si dovrà anche
calcolare opportunamente la distanza PP' (non necessariamente opposti
rispetto al centro della Terra) e le conseguenze geometriche nella
valutazione e risoluzione del triangolo. Difficoltà di calcolo
che non hanno comunque impedito un efficace impiego del metodo. |