|
|
|
|
|
|
|
|
|
La distanza della Luna
Claudio
Elidoro
|
La prima considerazione, come promesso
al lettore, è giustificare nei dettagli quel valore di 30 diametri terrestri
ottenuto da Aristarco per la distanza Terra-Luna. Si è detto che il
diametro apparente della Luna è contenuto 720 volte nel suo percorso sulla volta
celeste. A ben guardare, però, tale percorso è una circonferenza centrata
nella Terra e il cui raggio è proprio la distanza Terra-Luna. Chiamando
dunque dTL la distanza
Terra-Luna e DL il
diametro lunare, possiamo scrivere che DL
× 720 = 2p × dTL da cui possiamo immediatamente
ricavare che dTL
= (DL × 720) / 2p Se, in accordo con le
osservazioni sulle eclissi, mettiamo a questo punto in conto il fatto che il
diametro terrestre (DT)
è pari a quattro volte quello lunare, otteniamo che dTL
= (DT × 90) / p
~ DT
× 30 Obiettivo di una seconda
considerazione è quello di ricordare un altro famoso tentativo nella
determinazione della distanza lunare, quello compiuto da Ipparco di Nicea
(190-127 a.C.), altra colonna portante dell’astronomia antica. Anche le
considerazioni di Ipparco si basano su un’eclisse, questa volta, però, si
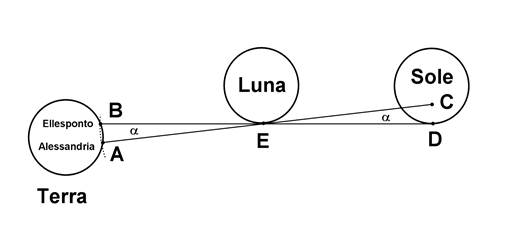
tratta di un’eclisse solare. Osservando accuratamente l’allineamento del
bordo lunare con il disco solare sia da Alessandria che dall’Ellesponto (vedi
Fig. 1), Ipparco riuscì a valutare
la parallasse del bordo lunare (punto E in figura) ottenendo un valore pari a
circa 1/5 del diametro apparente del Sole.
Fig. 1. Visto che il Sole sottende
circa mezzo grado, Ipparco dedusse per l’angolo a
il valore di circa 1/10 di grado. Poco probabile che l’astronomo di Nicea
conoscesse la distanza che separa l’Ellesponto da Alessandria (il tratto AB
nella figura), certo, invece, che fosse in grado di misurare la differenza
delle due latitudini (circa 9 gradi). Questa valutazione, chiamando rT il raggio terrestre,
suggeriva che AB = 9 (2p × rT)
/ 360 Il tratto AB, però, può essere
ricondotto anche a un’altra circonferenza oltre a quella del meridiano
passante per Alessandria e l’Ellesponto. Si tratta della circonferenza che ha
centro in E e raggio pari alla distanza Terra-Luna (dTL). Esprimendo dunque AB rispetto a questa
circonferenza e ricordando che l’angolo a vale 1/10 di grado, otteniamo che AB = 0,1 (2p × dTL)
/ 360 Uguagliando le due espressioni e
semplificando, Ipparco ottenne dTL/rT = 90. Giunse cioè a stabilire che la distanza
della Luna fosse pari a 90 raggi terrestri, sovrastimandola dunque di circa
il 50%. Un’importante causa di tale errore la possiamo identificare
facilmente: il tratto AB valutato lungo il meridiano non è uguale al tratto
sotteso dall’angolo a.
Rifacendo dunque i calcoli tenendo conto della debita correzione si ottiene
il valore più accettabile di circa 70 raggi terrestri. Stando a quanto
affermano alcuni storici dell’astronomia, in realtà il valore ottenuto da
Ipparco sarebbe compreso tra 62 e 73 raggi terrestri. Il che, considerando la
difficoltà nell’apprezzare gli angoli in gioco, non può che suscitare un
profondo stupore per l’incredibile lavoro dell’astronomo di Nicea. |