|
|
|
|
|
|
|
|
|
Biciclette, trottole, stagioni
Annibale
D’Ercole
|
Chiunque
abbia avuto modo di giocare con una trottola sarà rimasto affascinato dalle proprietà
“misteriose” del suo moto. Se la trottola non ruota attorno al suo asse, essa
si comporta prevedibilmente: per quanto si tenti di porla in equilibrio
verticalmente – “in piedi” sul pavimento –essa cade inevitabilmente di
fianco. Ma, se ruota, il suo asse si inclina solo di poco e rimane stabile
senza “coricarsi” in terra. Inoltre, la trottola comincia a precedere, ovvero il suo asse non
punta sempre nella stessa direzione, ma la sua estremità superiore “disegna”
un cerchio parallelo al pavimento. Cosa impedisce alla trottola di cadere? E
cosa la spinge a precedere? Semplicemente, la sua inerzia. Gli
effetti dell’inerzia di un corpo sul suo moto traslatorio rientrano nella nostra
quotidianità e ci appaiono del tutto naturali. Se dobbiamo spingere la nostra
automobile in panne, sappiamo che compiremo un certo sforzo per comunicarle
una qualche velocità. Una volta posta in moto, però, non faremo più alcuna
fatica (stiamo assumendo la completa assenza di attrito e l’assoluta
orizzontalità della strada); al contrario, ora dovremo sforzarci se vogliamo
fermarla, spingendo in direzione opposta al suo moto. Questo semplice esempio
è la riprova di quanto stabilito dalla prima legge della dinamica di Newton:
in assenza di forze esterne, ogni corpo tende a mantenere il suo stato di
quiete o di moto rettilineo e uniforme. Questa tendenza è proprio l’inerzia,
ed è proporzionale alla massa del corpo (come è facile rendersene conto, se
si pretende di spingere un autotreno invece di una Cinquecento!). Nel
caso del moto rotatorio, anziché traslatorio come quello dell’esempio
precedente, l’inerzia produce effetti meno intuitivi e apparentemente
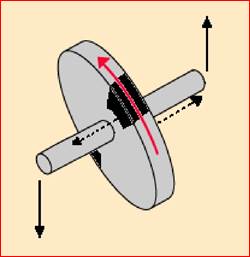
inspiegabili. In Fig. 1 viene
schematizzato un disco in rotazione, al cui mozzo viene applicata una
torsione (una coppia di forze rappresentata dalla coppia di frecce orientate
verticalmente) nel tentativo di variarne la direzione in senso antiorario.
Fig. 1. Applicando una
torsione (coppia di forze rappresentate dalle due frecce verticali) che tenda
a ruotare il mozzo del disco in rotazione, si comunica un impulso laterale
(coppia di frecce tratteggiate) ai settori indicati in nero. Fissiamo
ora l’attenzione sull’elemento di disco più alto (indicato in figura dalla
regione nera superiore). In assenza di forze esterne, esso tende a proseguire
in avanti lungo il suo moto circolare in base alla sua inerzia, come
stabilito dalla prima legge di Newton discussa in precedenza. L’applicazione
di una coppia di forze al mozzo si traduce, in pratica, in un impulso che
spinge l’elemento del disco verso sinistra (freccia tratteggiata in alto in Fig. 1). Sempre a causa della sua
inerzia, l’elemento conserva questa tendenza a muoversi lateralmente mentre
ruota attorno al mozzo. Quando, dopo mezzo giro, l’elemento in questione si
ritrova nel punto inferiore del disco, la sua inerzia tende a spingerlo a
sinistra, in opposizione alla torsione che invece tende a muoverlo verso
destra. Per l’elemento di ruota inizialmente più basso (zona nera inferiore
in Fig. 1) vale un ragionamento
simmetrico. Dunque, si crea una sorta di retroazione per cui, dopo mezzo
giro, l’impulso laterale fornito dalla torsione provoca una resistenza
all’ulteriore azione della torsione stessa. Questa
tendenza dei corpi rotanti a mantenere inalterata la direzione del proprio
asse di rotazione, resistendo alle perturbazioni esterne, viene utilizzata in
svariate applicazioni. La più comune è la bicicletta, che non cade mentre è
in moto perché le sue ruote, girando, tendono a mantenere orizzontale il
proprio mozzo. Giroscopi (sorta di trottole) elettrici vengono posti sulle
navi per favorire il mantenimento della direzione di marcia. Anche il
telescopio spaziale Hubble, in orbita attorno alla Terra, fa uso di giroscopi
per stabilizzare il proprio assetto. Sottolineiamo, inoltre, che il regolare
succedersi delle stagioni dipende dal fatto che Consideriamo
di nuovo il nostro disco e supponiamo che, inizialmente, il suo mozzo sia
parallelo al terreno con uno dei due estremi agganciato ad una corda (che
pende dall’alto) tramite uno snodo attorno al quale è libero di muoversi in
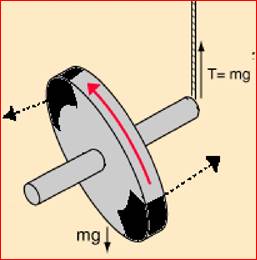
ogni direzione (Fig. 2).
Fig. 2. Situazione
analoga a quella illustrata in Fig.
1. In questo caso la torsione è dovuta alla gravità e alla tensione della
corda. Il disco è ruotato di un quarto di giro e i settori in nero si sono
posti orizzontalmente. In
assenza di rotazione, il disco cade penzolando dalla corda, col mozzo in
posizione verticale. Se però il disco gira su se stesso, il mozzo rimane
parallelo al terreno; esso inoltre precede, acquista cioè una rotazione
orizzontale attorno allo snodo, analoga alla rotazione di una lancetta di
orologio attorno al perno centrale. Il mozzo rimane orizzontale perché, come
ormai sappiamo, a causa della propria inerzia il disco tende a mantenere
inalterata la direzione del proprio asse di rotazione. E l’inerzia è
responsabile anche della precessione, come si può capire guardando Abbiamo già
detto della precessione della trottola. Anche |