Biciclette, trottole, stagioni
Annibale D’Ercole

La fisica degli oggetti rotanti è alquanto complessa, e una sua trattazione, sia pure semplificata, è decisamente al di là degli scopi di questa rubrica. Qui ne diamo solo brevi cenni, senza pretesa di rigore e di completezza, allo scopo di introdurre il lettore nel quadro logico in cui è inserita la dinamica dei corpi rotanti. Nel seguito, a meno di esplicite eccezioni, ci riferiremo solo a corpi rigidi, ovvero corpi che non si deformano sotto l’azione di forze esterne.

Se spingiamo con una forza F un oggetto di massa m sopra una superficie, imprimiamo a quest’ultimo una velocità υ via via crescente in direzione della forza stessa. La variazione di velocità (ovvero, l’accelerazione) termina quando smettiamo di spingere, e, in assenza di attrito, l’oggetto continua a viaggiare a velocità costante. Questa semplice immagine esemplifica la seconda legge di Newton che può essere scritta in maniera succinta come

, (1)

dove il punto sulle variabili indica la loro variazione temporale e dunque, ad esempio, indica la variazione della velocità nel tempo, ovvero l’accelerazione. L’ultimo passaggio nell’equazione precedente deriva dalla definizione di quantità di moto di un oggetto, che è data da q = mυ (quest’ultima formulazione della legge di Newton ci sarà utile tra poco). Per quanto abbiamo detto prima, in assenza di forza (F = 0), la velocità e l’impulso rimangono costanti. In termini matematici, questo significa che, in base all’equazione (1), , ovvero

(2)

È importante sottolineare che la velocità (come peraltro la forza e la quantità di moto) è un vettore, che può essere rappresentato da una freccia la cui direzione coincide con la direzione del moto, e la cui lunghezza, detta modulo, è proporzionale al valore della velocità (una freccia che rappresenta una velocità di 60 km/h ha una lunghezza doppia rispetto ad una freccia che indica una velocità di 30 km/h). Come abbiamo appena visto, l’applicazione di una forza nello stesso verso della velocità di un corpo (o nel verso opposto) produce un aumento (o una diminuzione) della velocità, che però mantiene inalterata la propria direzione. Può tuttavia accadere che la forza venga applicata in direzione perpendicolare alla velocità; in questo caso il modulo della velocità (la lunghezza della freccia che la rappresenta) non cambia, mentre cambia la sua direzione. Se imprimiamo una velocità a un oggetto collegato, tramite una corda, a un perno centrale, produciamo un moto circolare attorno al perno stesso, causato dalla tensione della corda che “tira” l’oggetto perpendicolarmente alla velocità. In assenza di attrito, l’oggetto non rallenta e dunque la velocità mantiene costante il suo modulo, ma cambia continuamente direzione. Questo caso è il complementare del precedente, in cui il vettore velocità varia il proprio modulo ma non la direzione.

Consideriamo ancora un oggetto in orbita circolare (Fig. 3) e diamo una serie di definizioni che potranno apparire cervellotiche e noiose … preghiamo tuttavia il lettore di avere pazienza: tra poco ne capirà le ragioni.

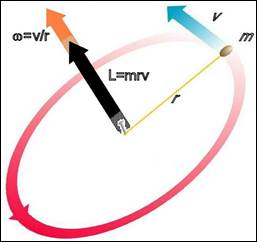
Fig. 3. Un oggetto in orbita circolare con velocità υ possiede una velocità angolare w e un momento angolare L = mrυ. Questi due vettori sono entrambi perpendicolari al piano dell’orbita e diretti come indicato nella figura. Se la rotazione illustrata fosse stata in senso orario, L e w avrebbero il verso opposto.

Oltre alla velocità lineare è possibile definire la velocità angolare ω che indica il numero di giri eseguiti dal corpo nell’unità di tempo: è facile verificare che la relazione tra queste due velocità è data da υ = rω, dove r è il raggio dell’orbita circolare. È inoltre possibile definire il momento della quantità di moto – o momento angolare – come

L = rq = rmυ = mr²ω = Iω;

l’ultimo passaggio tiene conto di un’ulteriore definizione, quella del momento di inerzia I = mr². Per definizione, L e ω sono due vettori entrambi paralleli all’asse attorno a cui ruota il corpo (Fig. 3). Finalmente, diamo l’ultima definizione necessaria per il nostro discorso, quella del momento della forza: se applichiamo all’oggetto raffigurato in Fig. 3 una forza F diretta come la velocità indicata nella stessa figura, il momento della forza è dato da τ = rF ed è rappresentato da un vettore diretto come L e ω (si confrontino la Fig. 3 e lo schema mostrato nella regione sinistra della Fig. 4).

Fig. 4. A sinistra è evidenziata la relazione tra momento della forza t e la variazione DL di momento angolare L di un disco (dato dalla somma dei momenti angolari dei suoi singoli elementi) in un intervallo di tempo Dt nel caso che t e L siano paralleli. Lo schema a sinistra illustra il caso in cui t e L siano ortogonali. Vale la relazione DL=Dt.

Naturalmente, al crescere di τ cresce anche (ovvero la rapidità con cui varia ω), come è intuitivo e come è facile verificare moltiplicando per r entrambi i membri dell’equazione (1):

, (3a)

. (3b)

Da questa equazione si capisce che, in assenza di un momento di una forza agente su un oggetto rotante (t = 0), la velocità angolare dell’oggetto stesso non cambia (), così come non cambia il suo momento angolare (); analogamente a quanto abbiamo visto per l’equazione (1), otteniamo:

(4)

C’è una certa analogia tra l’equazione (2) e l’equazione (4); la prima ci dice che un corpo mantiene costante la propria velocità (sia in modulo che in direzione) in assenza di forze esterne, la seconda che un oggetto in rotazione mantiene costante il proprio momento angolare (sia in modulo che in direzione) in assenza di un momento della forza. Il momento angolare di una ruota di una bicicletta in moto è allineato con il mozzo della ruota e dunque è parallelo al terreno. Proprio la sua tendenza a mantenere inalterata questa direzione permette di andare in bicicletta senza cadere.

Vi è, comunque, un’importante differenza tra l’equazione (2) e l’equazione (4): mentre la massa m rimane costante, il momento di inerzia I può variare. Nel caso di corpi deformabili, un eventuale cambiamento della distanza r di alcune delle loro parti dall’asse di rotazione implica una variazione di I: questa variazione deve essere compensata da un cambiamento di ω in maniera che il momento angolare rimanga costante, come imposto dall’equazione (4). Una pattinatrice sul ghiaccio che inizi a ruotare su se stessa, tenendo le braccia tese orizzontalmente, girerà sempre più velocemente avvicinando le braccia al corpo (ovvero diminuendo il proprio momento d’inerzia), senza che intervengano forze esterne, ma solo in virtù della conservazione del momento angolare.

Veniamo ora al fenomeno della precessione. Abbiamo visto che una forza applicata a un corpo parallelamente alla sua velocità varia il modulo di quest’ultima, ma non la sua direzione; se invece la forza è ortogonale alla velocità, ne varia la direzione, ma non il modulo. Analogamente, un momento della forza parallelo al momento angolare di un corpo in rotazione ne varia il modulo, ma non la direzione, mentre un momento della forza ortogonale al momento angolare ne varia la direzione, ma non il modulo. 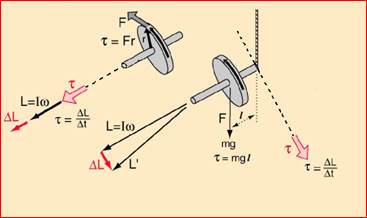Il primo caso lo abbiamo già discusso ed è esemplificato nella parte sinistra della Fig. 4. Il secondo caso è pure illustrato nella stessa figura. Consideriamo un disco in rotazione con il mozzo parallelo al terreno; uno dei due estremi è vincolato a una corda che lo sorregge, mentre l’altro è libero di muoversi. Il disco è sottoposto a un momento della forza dovuto alla gravità che agisce sul baricentro del disco: t = lmg, dove l è la semilunghezza del mozzo, m la massa del disco e g l’accelerazione di gravità. Per quel che abbiamo detto in precedenza, t è orientato ortogonalmente a l, e dunque a L. Pertanto, il momento della forza non cambia il modulo della velocità angolare del disco, che continua a girare con la stessa rapidità; ne cambia però la direzione, “tirando” il mozzo dalla propria parte e dando così origine alla precessione, ovvero al moto di rotazione orizzontale del mozzo attorno all’estremità vincolata alla corda.

---

Home Spigolature

Livello Base