|
|
|
|
|
|
|
|
|
Fornaci nucleari
Claudio
Elidoro
|
Proviamo a scorgere qualche dettaglio
più fine nel disegno che abbiamo tracciato finora. La prima domanda che
potremmo porci ci viene suggerita dalle immagini tristemente familiari delle
esplosioni termonucleari. Noi sappiamo che in quegli eventi si verificano le
reazioni di fusione nucleare che avvengono anche nel Sole e nelle altre
stelle, ma non per questo il Sole – fortunatamente per noi – esplode in un
botto. Uno dei motivi va ricercato nella straordinaria lentezza della prima
reazione del ciclo protone-protone. Nonostante la scorciatoia costituita
dall’effetto tunnel, infatti, sono mediamente necessari miliardi di anni
perché i primi due protoni della catena si uniscano a formare un nucleo di
deuterio. Non solo è necessario che venga superata la barriera di potenziale
coulombiano tra i due protoni, ma deve anche avvenire la trasformazione di
uno dei protoni in neutrone (emettendo un positrone e un neutrino) in modo che
il nucleo che si viene a formare sia stabile. Nel Sole e nelle stelle queste
difficoltà vengono superate grazie alla disponibilità oltremodo smisurata di
protoni. Un ulteriore elemento
sul quale porre la nostra attenzione deriva da un confronto diretto tra il
ciclo protone-protone e il ciclo CNO. Già si è avuto modo di osservare che il
ciclo protone-protone è di gran lunga predominante nelle stelle meno calde,
una circostanza che dipende dal fatto che le barriere coulombiane presenti
nelle reazioni del ciclo CNO sono molto più elevate e dunque il loro
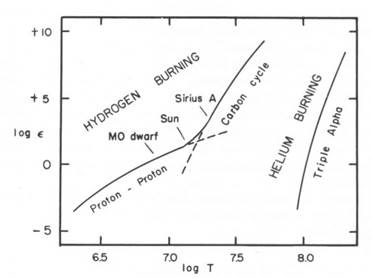
superamento richiede energie (cioè temperature) più alte. Osservando in un
grafico logaritmico temperatura-energia l’andamento dei due cicli (vedi Fig.
3) possiamo però notare anche un’altra caratteristica.
Fig. 3. Produzione di energia nucleare in funzione
della temperatura (da M. Schwarzschild, Structure and evolution
of the stars, Princeton University Press, 1958). La maggiore quantità di
energia liberata e la pendenza più elevata della curva relativa al ciclo CNO
indicano come questo meccanismo sia molto più efficiente della catena
protone-protone. Approssimando in modo piuttosto drastico la produzione di
energia con una espressione del tipo E µ Tn si ottiene che nel caso della catena
protone-protone l’esponente n ha
un valore tipico di 4 mentre nel caso del ciclo CNO ha valore 14. Abbandoniamo ogni
ulteriore approfondimento (che richiederebbe di mettere in gioco oltre alla
temperatura anche la densità e la composizione chimica del materiale
stellare) e proviamo a valutare, come è stato fatto in una precedente Spigolatura con gli altri possibili combustibili stellari, la correttezza e la
tenuta dell’ipotesi che stiamo esaminando. Proviamo, in altre parole, a fare
i conti in tasca alla fornace nucleare del Sole. Il punto di partenza può
essere quel difetto di massa individuato da Aston dal confronto tra quattro
atomi di idrogeno e uno di elio e valutato in Dm = 0,048 x10 Grazie all’equivalenza
massa-energia introdotta da Einstein, possiamo esprimere quel difetto di
massa in termini energetici ottenendo DE = Dm c2 = 4,3 x 10-5 erg. Valutando il rapporto
tra questo dato e la massa di un atomo di elio otteniamo un’indicazione
attendibile dell’efficienza della fusione dell’idrogeno. Pertanto:
Possiamo a questo punto
valutare per quanto tempo la fornace del Sole è in grado di sostenere la sua
produzione di energia. Se ipotizziamo che il Sole (MSole
= 2 x
Abbiamo più volte avuto
modo di vedere come l’energia bruciata ogni secondo dal Sole (sostanzialmente
la sua luminosità) ammonti a 4 x
1033 erg/s. Il rapporto tra la disponibilità teorica di energia e
il suo consumo può dunque indicarci per quanto tempo l’energia di fusione
potrebbe sostenere il Sole. Facendo i conti otteniamo:
Il valore ottenuto (100
miliardi di anni) è una prova concreta che, a differenza di quanto trovato
analizzando altre fonti energetiche, questa volta non abbiamo alcun problema
di tempo. Il nostro semplice calcolo ci indica che l’energia di fusione
nucleare non solo è abbondantemente in grado di assicurare la produzione
energetica del Sole dalla sua formazione fino ai nostri giorni, ma anche che
potrà sostenerlo per molto tempo ancora. |