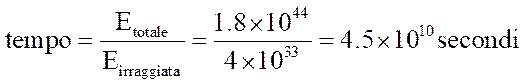|
|
|
|
|
|
|
|
|
Il carburante delle stelle
Claudio
Elidoro
|
Come abbiamo fatto in precedenti occasioni, proviamo ad
approfondire il discorso aiutandoci con qualche semplice calcolo. Si è già
avuto modo di sottolineare come ogni possibile metodo di produzione di
energia possa in prima battuta essere preso seriamente in considerazione solo
se è in grado di restare attivo per un tempo compatibile con il tempo
evolutivo caratteristico del Sole e del Sistema solare. Valutiamo dunque
concretamente il “tempo di funzionamento” del Sole considerando le differenti
sorgenti energetiche che abbiamo ipotizzato in precedenza. 1. Combustione Se ipotizziamo una combustione del tipo
la produzione di energia che ne deriva è di 9x1010 erg/g. Perché tutto funzioni il Sole dovrebbe
essere composto per il 27% di carbonio e per il restante 73% di ossigeno. Sorvoliamo
sulla stranezza di una simile composizione e proviamo a calcolare il
contenuto energetico complessivo. Poiché la massa del Sole è di 2x1033 grammi, otteniamo che,
complessivamente, la nostra stella, fatta di carbonio e ossigeno, potrebbe
liberare (9x1010 x 2x1033) = 1.8x1044 erg. Conoscendo quanta energia irraggia il
Sole (LSOL= 4x1033
erg/s) possiamo agevolmente calcolare quanto tempo può restare accesa quella
fornace:
Poiché un anno corrisponde a 3.15x107 secondi, la combustione
di un Sole di carbonio e ossigeno può al massimo protrarsi per 1428 anni. La situazione non migliora di molto
anche ipotizzando che l’intero Sole possa essere tutto di carbone (per
esempio di antracite, il cui potere calorico è di 3.8x1011 erg/g) e l’ossigeno
necessario alla combustione venga assicurato dall’ambiente esterno (!).
Otterremmo: ETOT = 2x1033 x 3.8x1011 = 7.6x1044 erg Ripetendo i calcoli precedenti
impiegando il nuovo valore del contenuto energetico del Sole otteniamo per il
tempo di combustione il valore di 1.9x1011 secondi, vale a dire 6031 anni. 2. Contrazione
gravitazionale Il contenuto di energia potenziale di una stella nel
proprio campo gravitazionale è dato dalla seguente espressione:
Inserendo i valori della costante di
gravitazione universale, della massa e del raggio del Sole otteniamo un
contenuto energetico pari a 2.3x1048
erg. Se ora immaginiamo che questa energia
venga completamente convertita in energia radiante e calcoliamo – come in
precedenza – la possibile durata (T) di una simile fase otteniamo:
valore che corrisponde a 1.8x107 anni. Non v’è alcun
dubbio che la nuova situazione porti un deciso miglioramento rispetto
all’ipotesi precedente, ma siamo ancora molto lontani dal poter considerare
questo meccanismo il responsabile della attuale produzione energetica del
Sole. 3. Ipotesi
meteoritica L’ultimo esercizio di calcolo che
affrontiamo riguarda la cosiddetta ipotesi meteoritica. Si è detto che il
meccanismo fisico che sta alla base di questa ipotesi è la trasformazione
dell’energia cinetica posseduta da un oggetto in energia termica. Proviamo
dunque a valutare l’entità di questa pioggia meteoritica per garantire la
produzione energetica attuale del Sole. Ipotizzando una velocità di caduta di circa 618 km/s
(valore che corrisponde alla velocità di fuga dal Sole) calcoliamo l’energia
cinetica posseduta da un grammo di materia. Otteniamo:
Per garantire l’attuale produzione di
energia, dunque, ogni secondo dovrebbero cadere sul Sole
quantità che in un anno ammonterebbe a 2.1x1018 x 3.15x107 = 6.6x1025 grammi. Ricordando che la massa della Terra è
5.98x1027 grammi, significa che,
per garantire l’attuale produzione energetica del Sole ricorrendo all’ipotesi
meteoritica, all’incirca ogni 100 anni dovrebbe sparire dalla circolazione –
inghiottito dal Sole – un pianeta grande quanto Davvero un po’ troppo. |