|
|
|
|
|
|
|
|
|
Il caos
Annibale
D'Ercole
Osservatorio
Astronomico - Bologna
|
Supponiamo di impartire ad una pallina
poggiata su di un piano una velocità in una direzione ben precisa. La pallina
si muoverà lungo questa direzione seguendo una traiettoria rettilinea. Se ora
ripetessimo l’esperimento con una seconda pallina, sarebbe praticamente
impossibile — nonostante ogni sforzo da parte nostra — impartirle la stessa identica direzione di moto. Un
piccolo errore nel lancio iniziale si rifletterebbe in una traiettoria
rettilinea leggermente divergente rispetto alla precedente: tale divergenza
sarebbe tanto minore quanto minore è stato lo scarto nelle velocità iniziali.
Questo ci appare alquanto banale e riflette la nostra aspettativa che quanto
più simili sono le condizioni di partenza, tanto più simili saranno le
successive evoluzioni di un sistema fisico. Supponiamo ora di
porre la nostra pallina sul crinale di un tetto e di volerle imporre una
velocità esattamente parallela al crinale, in modo da farla muovere lungo di
esso. Questo richiederebbe da parte nostra una precisione di lancio
enormemente superiore alle nostre capacità: una qualche imprecisione, per
quanto piccola, sarebbe inevitabile. Se, ad esempio, la velocità iniziale
divergesse, sia pure di pochissimo, verso destra, dopo un tragitto più o meno
lungo (che dipende dalla nostra accuratezza) la pallina scivolerebbe via dal
crinale verso destra e rotolerebbe in terra a diversi metri dal crinale
stesso. Se lo stesso errore lo avessimo compiuto verso sinistra, la pallina
si ritroverebbe alla stessa distanza dal crinale, ma in direzione opposta
alla precedente. In conclusione, in questo esempio una sia pure
impercettibile differenza nelle condizioni iniziali porta il sistema ad
evolvere in maniera completamente diversa. Nonostante la forza di gravità
agente sulla pallina sia perfettamente descrivibile, a causa dell’elevata
sensibilità alle condizioni iniziali la traiettoria di quest’ultima è di
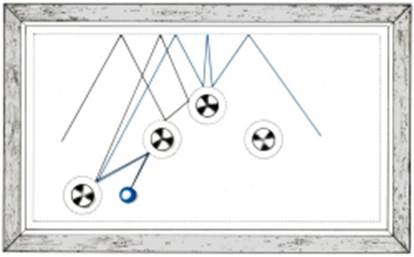
fatto impredicibile. Un altro semplice
esempio di sistema impredicibile è dato dall’urto tra palle di biliardo: la
fig. 1 mostra come una piccola variazione nella direzione della velocità
iniziale di una palla porta, al succedersi degli urti, ad una traiettoria
completamente diversa. Sistemi di questo genere, fortemente dipendenti dalle
condizioni iniziali, vengono detti caotici,
e rappresentano la norma in natura.
Grazie alle leggi
della dinamica scoperte da Newton, Halley fu effettivamente in grado di
tracciare l’orbita della cometa osservata nel 1682, che da lui prende il
nome, prevedendone esattamente la data del ritorno. Tuttavia, questo fu
possibile solo perché il sistema Sole più cometa (l’influenza dei pianeti è
trascurabile in questo caso) è particolarmente semplice. Ma se il Sole fosse
stato una stella binaria con una compagna di massa paragonabile, Halley non
avrebbe potuto fare alcuna previsione nonostante la forza di gravità totale
agente sulla cometa sia facilmente calcolabile anche in questo caso. Gli
inevitabili errori di misura nel determinare la posizione e la velocità della
cometa di Halley, per quanto piccoli, avrebbero introdotto incertezze
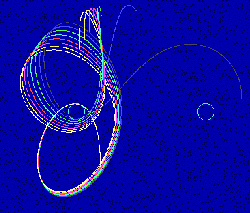
intollerabili nella previsione della traiettoria. La fig. 2 mostra quanto
consistenti possano essere le variazioni della traiettoria di un oggetto
sottoposto alla gravità di due stelle (i due cerchi in figura) al minimo
variare della sua velocità di partenza.
Gli astronomi
ritengono che alcuni sottosistemi del Sistema solare abbiano un comportamento
caotico. La regione compresa tra Marte e Giove è occupata dalla fascia di
asteroidi che tuttavia non è uniformemente popolata, ma presenta zone in cui
gli asteroidi mancano. L’influenza del vicino Giove rende instabili le orbite
comprese in queste zone e gli eventuali asteroidi che vi transitano sono
destinati ad allontanarsi. L’obliquità di Marte (l’angolo tra l’asse di
rotazione ed il piano orbitale) varia in maniera altamente irregolare su
scale temporali di quattro milioni di anni. Caotiche sono anche le orbite di
Iperione, un satellite di Saturno, e dei satelliti di Giove ed Urano. Non è
escluso che a lungo andare lo stesso Sistema solare nel suo insieme diventi
caotico. La cosa non sfuggì al genio di Newton il quale, tuttavia, riteneva
che Dio intervenisse di tanto in tanto a stabilizzare le orbite planetarie. Ma
il caos può verificarsi in molti altri campi della fisica ed anche in settori
lontani dalle cosiddette scienze esatte. La turbolenza dei fluidi, le aritmie
cardiache, le improvvise oscillazioni nella popolazione di una specie o nella
diffusione di una malattia oppure nella concentrazione degli elementi in
alcune reazioni chimiche o nell’andamento economico di alcune merci sono
tutte manifestazioni di sistemi caotici. Supponiamo di iniettare, tramite un
ugello sottile, una piccola corrente di acqua colorata in un liquido
incolore, per esempio acqua, che fluisce in un condotto di vetro. Se la
velocità del fluido non è molto elevata, la corrente colorata forma un
filetto che scorre parallelamente al condotto senza omogeneizzarsi con il
liquido circostante. Se la velocità supera un certo valore, il filetto, pur
mantenendo la propria identità, mostra delle oscillazioni. Un ulteriore
aumento della velocità porta a raddoppiare le frequenze di oscillazione.
Continuando ad aumentare la velocità si assiste ad un aumento a cascata delle
frequenze di oscillazione finché, superata una velocità critica, il moto da
laminare diventa irregolare con la formazione di vortici e conseguente
completo rimescolamento delle due correnti liquide. Per
quanto possa sembrare strano, l’andamento temporale della popolazione di
certe specie all’interno di alcuni ecosistemi può essere assimilato a quello
della turbolenza appena illustrato. Se il numero di predatori (ad esempio le
volpi) è piccolo rispetto a quello delle prede (per esempio i conigli), i
predatori aumenteranno fino a raggiungere un equilibrio tra prede e
predatori. Se la fertilità aumenta, la popolazione si stabilizza su un
livello più alto. Il superamento di un certo valore critico della fertilità,
tuttavia, porta le popolazioni di prede e predatori a non essere più stabili
e ad oscillare nel tempo tra due determinati valori. Un ulteriore aumento
della fertilità conduce ad un aumento delle oscillazioni delle popolazioni,
finché, superata una fertilità critica, l’andamento delle popolazioni sarà
completamente caotico. Un simile comportamento è stato effettivamente
riscontrato, in un periodo di più di cento anni a cavallo tra il secolo
scorso e quello precedente, nell’evoluzione delle popolazioni delle lepri
delle nevi (prede) e delle linci (predatori) nel Canada. Anche alcuni episodi di diffusione di
determinate malattie infettive hanno mostrato un andamento caotico. Morbillo,
poliomielite e rosolia, ad esempio, presentano una frequenza di diffusione
che tende ad aumentare e diminuire a periodi. Ci si aspetta che
l’introduzione di un programma di vaccinazione porti direttamente ad una
riduzione dell’incidenza di queste malattie. In realtà, a seguito di una
campagna per estirpare la rosolia in Gran Bretagna, i medici hanno osservato
oscillazioni uguali a quelle descritte più sopra per l’andamento di certe popolazioni.
Un brusco aumento a breve termine dei casi di rosolia non indica
necessariamente un’inefficienza del vaccino, ma un’inevitabile reazione di un
sistema complesso. In
generale, per bassi valori di un determinato parametro — detto parametro d’ordine (la velocità
nell’esempio della turbolenza, la fertilità nel caso delle popolazioni di
prede e predatori) — l’evoluzione futura di un sistema può essere
determinata. All’aumentare del parametro d’ordine il sistema passa
dall’ordine al caos ed ogni predizione è praticamente preclusa. Come abbiamo
già detto, queste regole si applicano nei campi più disparati, dalla fisica
alla chimica, alla meteorologia, alla biologia, alla medicina, all’economia,
ecc. Proprio a causa di questa generalità, alcuni studiosi considerano la
teoria del caos la terza rivoluzione scientifica del secolo scorso, dopo la
teoria della relatività e la meccanica quantistica.
|