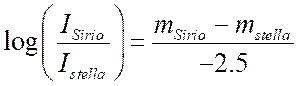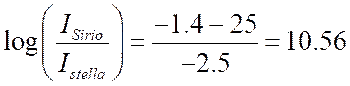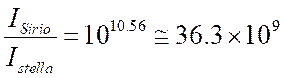La magnitudine stellare
Claudio Elidoro

La convenzione proposta da Pogson ipotizzava che una differenza di cinque classi di magnitudine corrispondesse esattamente ad un rapporto 100:1 dei flussi luminosi. Ma quale incremento di luminosità caratterizza il passaggio da una classe a quella successiva? I volonterosi possono fare i calcoli utilizzando l’equazione (2): è sufficiente inserire al posto di m e mo due numeri consecutivi, sostituire a k il valore numerico corretto (– 2.5) e risolvere rispetto al rapporto I/Io. Per chi non se la sente di accendere la calcolatrice riveliamo che il rapporto di flussi luminosi che si otterrà dal calcolo (limitando il risultato a quattro decimali) sarà di 2.5118:1.

Considerando le luminosità, dunque, siamo di fronte ad una progressione geometrica di ragione 2.5118, risultato al quale si poteva pervenire per altra via. Infatti, dato che il rapporto di luminosità di 100:1 copre un salto di 5 classi, si tratta di dividere il numero 100 in 5 parti tali che il rapporto tra due adiacenti rimanga costante. 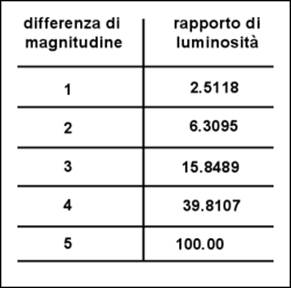Per fare questo dobbiamo calcolare la radice quinta di 100, che altro non è che 2.5118.

A questo punto siamo così in grado di comporre questa tabella riassuntiva:

 

 Fig. 2.

 

Approfittando della calcolatrice ancora accesa potremmo chiederci quante volte Sirio (m = –1.4) sia più luminosa di una stella di magnitudine 25 (traguardo accessibile solamente a un limitato numero di telescopi).

Avremo che:

 

da cui

 

E dunque:

 

 

Risultato certamente eclatante, ma che, comunque, non ci da assolutamente nessuna indicazione di tipo fisico sulle reale emissioni luminose delle due stelle.

Più interessante, invece, provare a fare due conti con la magnitudine assoluta.

Deneb (costellazione del Cigno) ha una magnitudine apparente di + 1.25 e si trova ad una distanza di 500 parsec. Proviamo a valutarne la magnitudine assoluta:

 

M Deneb = 1.25 + 5 – 5 log 500

            = 1.25 + 5 – 13.49 = –7.24

 

Facciamo ora un analogo calcolo per il Sole, sapendo che m Sole = – 26.74 e che la sua distanza da noi (1 UA) corrispondente a 1/206265 parsec [1].

 

M Sole = – 26.74 + 5 – 5 log (1/206265)

= – 26.74 + 5 + 26.57 = + 4.83

 

Ragionando sui risultati ottenuti possiamo dunque constatare che Deneb è quasi 70 mila volte più luminosa del Sole. Ancora non sappiamo a cosa imputare questo enorme divario, ma almeno siamo certi che non dipende dalla distanza.

Home
Spigolature

 

Livello
Base

 


[1]Espresso in radianti, 1 secondo d’arco è 1/206265.

Questo comporta che una stella con parallasse di 1 secondo d’arco si trova ad una distanza pari a 206265 volte l’Unità Astronomica (assunta come unità metrica della nostra misurazione). Volendo cercare il pelo nell’uovo si potrebbe obiettare che l’affermazione non è trigonometricamente corretta, ma con angoli così piccoli si può ragionevolmente approssimare il lato opposto all’angolo di parallasse all’arco di circonferenza sotteso.