Un campo elettrico oscillante con frequenza  si propaga nello spazio a velocità c
= 300.000 km al secondo. Queste oscillazioni possono essere descritte mediante la
formula E = Eocos (kx - si propaga nello spazio a velocità c
= 300.000 km al secondo. Queste oscillazioni possono essere descritte mediante la
formula E = Eocos (kx -  t), dove E rappresenta il campo
elettrico, k e t), dove E rappresenta il campo
elettrico, k e  sono due costanti, x e t
rappresentano lo spazio e il tempo. sono due costanti, x e t
rappresentano lo spazio e il tempo.
Questa formula indica che l’oscillazione si propaga ad x
crescenti con velocità c= /k. /k.
Per rendercene conto fissiamo ad esempio l’attenzione sulla cresta dell’onda,
ovvero sul valore massimo Eo raggiunto dal campo
elettrico durante l’oscillazione. Tale valore è ottenuto per ogni valore di x
e t per cui si ha kx- t=0; questa relazione può essere riscritta come x=( t=0; questa relazione può essere riscritta come x=( /k)t ed indica appunto
che, all’aumentare di t, la posizione della cresta si muove
verso x crescenti con velocità /k)t ed indica appunto
che, all’aumentare di t, la posizione della cresta si muove
verso x crescenti con velocità  /k. /k.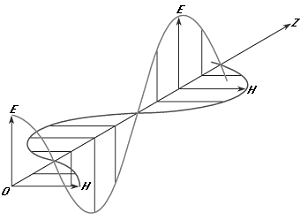
Supponiamo ora di "fotografare" l’onda ad un
determinato istante t' ; l’onda è descritta da una
sinusoide lungo x, e la distanza tra due massimi contigui posti
in due punti x1 e x2
definiscono la lunghezza d’onda 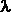 =x2-x1. =x2-x1.
Per quanto detto più sopra, deve essere kx2 -  t' = kx1 +2 t' = kx1 +2 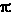 - -  t' = 0, perché, com’è noto, il coseno è una funzione
periodica di 2 t' = 0, perché, com’è noto, il coseno è una funzione
periodica di 2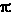 radianti, ovvero assume lo stesso valore per valori dell’argomento che differiscono
tra loro per multipli interi di 2
radianti, ovvero assume lo stesso valore per valori dell’argomento che differiscono
tra loro per multipli interi di 2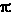 . Si ottiene pertanto k=2 . Si ottiene pertanto k=2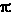 / / 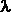 . .
Supponiamo ora di essere fermi in un determinato punto x' e di
misurare il periodo T dell’onda, ovvero il tempo che intercorre tra il
ripetersi di due massimi successivi che si verificano agli istanti t1
e t2. Con un ragionamento analogo al precedente si
ottiene
 = 2 = 2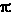 / T = 2 / T = 2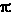  , dove , dove  = 1 / T è la frequenza
dell’onda. = 1 / T è la frequenza
dell’onda.
Da questi risultati si ricava la relazione tra frequenza, lunghezza d’onda e
velocità:
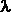  = c. = c.
Il campo elettrico, com’è noto, è una forza in grado
di accelerare particelle cariche comunicando loro energia. Dunque un’onda
elettromagnetica trasporta energia che viene trasferita a particelle cariche, ad esempio
elettroni, che si trovino lungo la sua traiettoria.
Si può dimostrare che l’intensità dell’onda - ovvero il flusso di
energia che si riversa ogni secondo su un centimetro quadrato di superficie di un corpo
investito dall’onda - è pari a F = Eo2 c /
8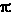 . .
Come si vede, questo flusso dipende dall’ampiezza, ma non dalla frequenza
dell’onda; una circostanza, questa, di importanza cruciale per le considerazioni che
stiamo per fare.
Gli elettroni nei metalli si prestano particolarmente ad
interagire con onde elettromagnetiche di opportuna energia. Infatti, nei metalli gli atomi
sono "impacchettati" in maniera tale che le loro orbite elettroniche si toccano
e si confondono. Pertanto un elettrone non è legato ad un particolare atomo, ma è libero
di scorrere da un atomo a l’altro: questo spiega l’alta conducibilità elettrica
dei metalli.
Naturalmente, nonostante la loro elevata mobilità, gli elettroni sono comunque vincolati
a rimanere all’interno dei metalli a causa dell’azione attrattiva combinata dei
nuclei atomici. Per riuscire ad estrarli è necessario comunicare loro
un’energia superiore all’energia U , detta potenziale
di estrazione, che rappresenta l’energia di legame tra nuclei ed elettroni e il cui
valore varia da un materiale all’altro.
Se dunque investiamo un metallo con un’onda elettromagnetica, ci aspettiamo che gli
elettroni che accumulano ciascuno un’energia superiore ad U
vengano estratti con un’energia cinetica K=0.5mv2,
dove v è la velocità dell’elettrone ed m
la sua massa; questa energia cinetica è pari alla differenza tra l’energia assorbita
dall’onda ed il potenziale U.
Questo fenomeno va sotto il nome di effetto fotoelettrico e si verifica
effettivamente in natura. Tuttavia le sue modalità sono diverse da quelle previste dalla
teoria ondulatoria della luce. Infatti si osserva che se la frequenza  è inferiore ad un valore è inferiore ad un valore  o, detto di soglia e
dipendente dal tipo di materiale, non si ha effetto fotoelettrico, per quanto intensa sia
la radiazione impiegata. Inoltre, per o, detto di soglia e
dipendente dal tipo di materiale, non si ha effetto fotoelettrico, per quanto intensa sia
la radiazione impiegata. Inoltre, per  > > o,
il numero degli elettroni estratti rimane costante, ma la loro singola energia cinetica
aumenta all’aumentare della frequenza. o,
il numero degli elettroni estratti rimane costante, ma la loro singola energia cinetica
aumenta all’aumentare della frequenza.
Questa dipendenza dalla frequenza è incomprensibile nell’ambito della teoria
ondulatoria della luce perché, come abbiamo detto, il flusso di energia elettromagnetica
non dipende dalla frequenza dell’onda incidente.
Nell’interpretazione quantistica la radiazione non è
composta da onde ma da "particelle" di energia dette fotoni. Ogni
fotone viaggia alla velocità della luce e trasporta un’energia Ev=h , dove h
è la costante di Plank e , dove h
è la costante di Plank e  la frequenza della radiazione.
la frequenza della radiazione.
In questo caso il flusso di energia trasportato da un raggio luminoso è dato da:
F = Nf h  c,
dove Nf è la densità dei fotoni che
compongono la radiazione. c,
dove Nf è la densità dei fotoni che
compongono la radiazione.
Se illuminiamo un metallo con una radiazione di frequenza opportuna - ovvero tale per cui Ev
> U - ogni fotone che scalza un elettrone gli fornisce un’energia K=Ev-U.
Dalla condizione Ev = U si ricava il valore
della frequenza di soglia  o=
U / h. o=
U / h.
Aumentare l’intensità della radiazione equivale ad aumentare Nf
, ma non l’energia dei singoli fotoni. Di conseguenza si avrà un aumento del flusso
di elettroni, ma non della loro singola energia; un risultato in perfetto accordo con i
dati sperimentali.
Si noti infine che dalla misura della velocità degli elettroni e dalla conoscenza del
potenziale di estrazione del materiale usato è possibile ottenere una misura della
costante di Plank: h = (K+U) /  . .
Il valore così ottenuto è in piena sintonia con quello derivato per altra via,
confermando la validità della descrizione quantistica.
|