E' impossibile dare in
questa sede una trattazione rigorosa di come si possa risalire al moto
dell’universo a partire dalla misura di luminosità delle SNIa. Diamo
tuttavia qui di seguito una traccia che permetta al profano di intravedere
i concetti e le difficoltà in cui si imbattono i cosmologi.
Consideriamo una stella di luminosità
assoluta costante L posta ad una distanza D
. La radiazione emessa si allontana dalla stella in tutte le direzioni.
Pertanto la quantità di energia che fluisce ogni istante attraverso
una superficie sferica di raggio D centrata sulla stella
deve essere uguale a L= 4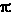 D2 D2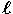 . .
La luminosità apparente
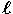 = L / (4
= L / (4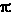 D2) D2)
dà una misura di come la stella
appaia sempre più fioca all’aumentare della distanza. Lo studio
delle SNIa vicine - la cui distanza è nota - ha permesso di stabilire
il valore di L, che risulta essere con buona approssimazione
sempre lo stesso per tutte le supernovae. Dalla misura di 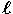 è allora possibile ricavare la distanza di una SNIa lontana tramite
la formula D
è allora possibile ricavare la distanza di una SNIa lontana tramite
la formula D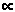 (L
/ (L
/ 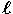 )1/2. )1/2.
Questi argomenti sono alquanto semplici
e funzionano bene per misurare, ad esempio, la distanza di oggetti all’interno
della nostra galassia o in galassie vicine. Se però consideriamo
sorgenti poste in galassie lontane non possiamo trascurare il moto di espansione
dell’universo. Sappiamo che una galassia posta a distanza D
si allontana con una velocità v proporzionale
a questa distanza secondo la legge di Hubble v=HoD
(dal nome dell’astronomo che per primo l’ha formulata), dove Ho
è detta appunto costante di Hubble.
E' altresì noto che la lunghezza
d’onda 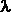 della radiazione
che giunge da una sorgente in allontanamento a velocità v
ci appare maggiorata di una quantità della radiazione
che giunge da una sorgente in allontanamento a velocità v
ci appare maggiorata di una quantità  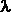 .
Questo fenomeno, detto effetto Doppler, è caratteristico dei fenomeni
ondulatori e si verifica anche nella percezione dei segnali sonori: la
sirena di un’ambulanza in allontanamento sembra meno acuta. .
Questo fenomeno, detto effetto Doppler, è caratteristico dei fenomeni
ondulatori e si verifica anche nella percezione dei segnali sonori: la
sirena di un’ambulanza in allontanamento sembra meno acuta.
L’incremento di lunghezza d’onda della
radiazione viene detto spostamento verso il rosso (red shift), e
viene misurato in termini percentuali tramite la variabile z=  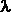 / / 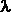 . .
Il red shift è tanto maggiore
quanto maggiore è la velocità di allontanamento della sorgente
secondo la relazione z=v/c, dove c è
la velocità della luce.
Torniamo ora alla determinazione della
distanza delle supernovae.
La luminosità apparente di
una supernova posta in una galassia che si va allontanando è data
da (si noti la comparsa del termine del red shift rispetto alla formula
data più sopra)
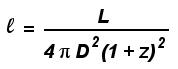
E' noto che l’energia trasportata dalla
radiazione è tanto minore quanto maggiore è la sua lunghezza
d’onda. Pertanto la luminosità apparente 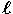 di una sorgente in allontanamento deve "affievolirsi" di un fattore (
di una sorgente in allontanamento deve "affievolirsi" di un fattore (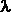 + +  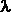 )/ )/ 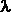 =(1+z)
a causa dell’effetto Doppler. Il secondo fattore (1+z) presente
nella formula cosmologica di =(1+z)
a causa dell’effetto Doppler. Il secondo fattore (1+z) presente
nella formula cosmologica di 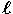 è dato dal ben noto effetto relativistico della dilatazione dei
tempi (si veda Spigolatura n.1/2000). L’orologio "agganciato" alla
sorgente che si allontana da noi corre più lentamente di quello
al nostro polso. Dunque il numero Nv di fotoni
emessi in un secondo (per la sorgente) ci raggiungeranno distribuiti su
di un intervallo temporale maggiore di un secondo per il nostro orologio.
è dato dal ben noto effetto relativistico della dilatazione dei
tempi (si veda Spigolatura n.1/2000). L’orologio "agganciato" alla
sorgente che si allontana da noi corre più lentamente di quello
al nostro polso. Dunque il numero Nv di fotoni
emessi in un secondo (per la sorgente) ci raggiungeranno distribuiti su
di un intervallo temporale maggiore di un secondo per il nostro orologio.
Dal momento che 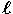 rappresenta l’energia che giunge ogni secondo (per il nostro orologio),
il numero di fotoni che arrivano durante uno dei nostri secondi si ottiene
riducendo Nv di un fattore che si dimostra facilmente
essere ancora (1+z).
rappresenta l’energia che giunge ogni secondo (per il nostro orologio),
il numero di fotoni che arrivano durante uno dei nostri secondi si ottiene
riducendo Nv di un fattore che si dimostra facilmente
essere ancora (1+z).
Dal confronto con la formula della
luminosità apparente per una sorgente immobile, si ricava che in
universo in espansione la distanza 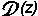 di una sorgente che presenta un red shift z è pari
a
di una sorgente che presenta un red shift z è pari
a
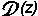 = D (1+z) = (c / Ho) z (1+z),
= D (1+z) = (c / Ho) z (1+z),
dove l’ultimo passaggio è stato
ottenuto utilizzando la relazione v = c z nella legge di
Hubble.
Nonostante l’estrema semplicità
di questi ragionamenti abbiamo ottenuto per la distanza un’espressione
assai simile a quella esatta
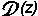 = (c / Ho) z (1+0.5 z)
= (c / Ho) z (1+0.5 z)
valida per un universo che si espande
senza rallentare, ovvero un universo in cui la gravità dovuta alla
materia presente è trascurabile.
In realtà noi non sappiamo quanta
materia c’è nell’universo; nel caso ve ne fosse in misura tale da
produrre un effetto frenante sull’espansione tramite la sua gravità,
il cosmo avrebbe dimensioni minori e la distanza 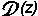 avrebbe una diversa dipendenza da z e sarebbe più
piccola.
avrebbe una diversa dipendenza da z e sarebbe più
piccola.
Dunque, per una data sorgente, l’espressione 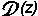 =(c
/ Ho) z (1+0.5 z) rappresenta la massima distanza possibile,
e la luminosità =(c
/ Ho) z (1+0.5 z) rappresenta la massima distanza possibile,
e la luminosità 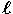 ad
essa associala la minima possibile. Questa considerazione è
assai importante per valutare i risultati osservativi esposti nella figura.
In essa vengono presentate le misure di ad
essa associala la minima possibile. Questa considerazione è
assai importante per valutare i risultati osservativi esposti nella figura.
In essa vengono presentate le misure di 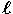 di numerose supernovae in funzione del valore di z mostrato
da ognuna.
di numerose supernovae in funzione del valore di z mostrato
da ognuna.
In realtà gli astronomi, in
analogia all’occhio che risponde logaritmicamente allo stimolo luminoso,
spesso descrivono l’energia ricevuta dalle sorgenti per mezzo della magnitudine
apparente definita come m = - 2,5log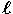 +cost +cost
Nel nostro caso, tenuto conto che
L può considerarsi costante per tutte le supernovae,
si ottiene m(z) = 5 log 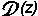 +K,
dove K è una costante (si noti che tanto maggiore
è la distanza, ovvero minore la luminosità apparente, tanto
maggiore risulta la magnitudine). +K,
dove K è una costante (si noti che tanto maggiore
è la distanza, ovvero minore la luminosità apparente, tanto
maggiore risulta la magnitudine).
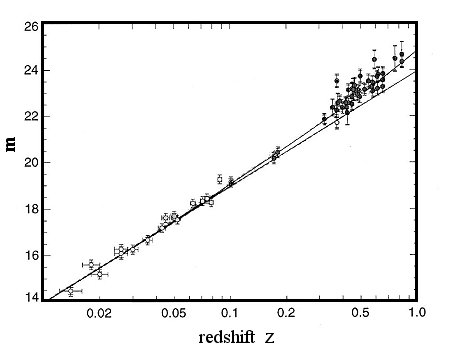
Questa è precisamente la quantità
graficata nella figura (adattata da Perlmutter et al., 1999, The Astrophysica
Journal, vol. 517, p. 565). In particolare, la linea superiore mostrata
nella figura illustra l’andamento di m(z) nel caso di un’espansione
"libera" (la formula ottenuta più sopra); la linea inferiore mostra
l’andamento della magnitudine apparente nel caso di un universo destinato
a rallentare l’espansione fino a invertire il moto e "richiudersi".
Fino ad un paio di anni fa le misure
erano limitate solo a supernovae con piccoli valori di z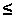 0,1
(cerchi chiari nella figura) e quindi, per la legge di Hubble, alquanto
vicine. Come si vede, queste misure non erano in grado di discriminare
tra i diversi modelli di universo. 0,1
(cerchi chiari nella figura) e quindi, per la legge di Hubble, alquanto
vicine. Come si vede, queste misure non erano in grado di discriminare
tra i diversi modelli di universo.
Grazie al telescopio spaziale (dedicato
proprio ad Hubble), di recente è stato possibile misurare la magnitudine
di supernovae più distanti (con 0,5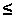 z z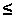 1). 1).
Il risultato è stato sconcertante.
Come si vede nella figura, al di là delle incertezze dovute agli
errori di misura (indicate dalle barre associate ai cerchi) la magnitudine
è risultata superiore (ovvero la luminosità è risultata
inferiore) di quella aspettata per un universo in espansione costante.
Questo significa che le distanze sono maggiori di quelle massime aspettate.
L’espansione dell’universo, dunque, non solo non viene rallentata dalla
gravità, ma viene anzi accelerata da una energia repulsiva indicata
con la costante cosmologica 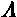 il cui significato fisico non è tuttavia ancora pienamente compreso.
il cui significato fisico non è tuttavia ancora pienamente compreso.
|