|
|
|
|
|
|
|
|
|
La gravità modificata (mond)
Annibale
D’Ercole
|
Come abbiamo detto nel livello base,
le stelle con velocità u
che orbitano circolarmente nel disco di una galassia a spirale, ad una
distanza r dal centro, sono sottoposte, da parte del bulge
di massa M, a un’accelerazione di gravità pari, secondo Newton, a GM/r2.
Queste stelle non cadono verso il centro, ma rimangono stabilmente a una
distanza r, perché l’accelerazione di gravità è controbilanciata
dall’accelerazione centrifuga ac = u2/r. Dall’eguaglianza di
queste due accelerazioni deriva Abbiamo detto che la
materia oscura giustifica l’eccessiva velocità con cui si muovono le stelle e
le galassie. Pertanto, la stragrande maggioranza degli astronomi è propensa a
credere alla sua reale esistenza, nonostante non si possa “vedere”
direttamente e neanche si sappia da cosa è composta. Una minoranza
d’astronomi, tuttavia, ritiene che la nostra attuale conoscenza della materia
oscura sia qualcosa di troppo “evanescente” per poterle conferire lo status
di realtà scientifica e preferisce spiegare le anomale velocità osservate,
ipotizzando che la gravità reale non sia descritta pienamente dalla formula
di Newton. In effetti, non è ancora stato possibile verificare la validità di
quest’ultima per valori molto bassi di g, inferiori a quelli misurabili
all’interno del Sistema solare. Siamo allora liberi di ipotizzare – come fa
la mond
– che, a grandi distanze dalla massa gravitante, g decresca come 1/r
piuttosto che come 1/r2. L’accelerazione di gravità si può allora
scrivere come dove L’equazione (1) è un’equazione
fenomenologica che introduce una nuova costante della natura, g0.
La forma precisa della funzione f(x) non è derivabile a priori e, in
realtà, non è molto importante. Tuttavia si richiede che i suoi comportamenti
asintotici siano i seguenti[2]: se
se
Pertanto, quando
l’accelerazione di gravità, calcolata secondo Newton, è molto maggiore di g0,
l’equazione (1) ricalca la formula di Newton; nel caso invece in cui
l’accelerazione newtoniana sia più piccola di g0 (GM/r 2<<
g0) si ottiene: Se, dunque, a grandi
distanze dal centro galattico utilizziamo l’equazione (2) per imporre l’equilibrio
tra accelerazione gravitazionale e centrifuga, otteniamo da cui Come si vede, in questo
caso la velocità circolare delle stelle non dipende dalla distanza. Inoltre,
risulta una chiara relazione tra u e g0 che permette di
calcolare quest’ultima, una volta che siano state misurate u
e M. Si ottiene g0 = 1.2×10-8 cm s-2. Questo
valore è circa 10 000 volte più piccolo dell’accelerazione di Plutone, la
minima accelerazione gravitazionale misurata; se fosse stato paragonabile,
avremmo dovuto già osservare nell’orbita di Plutone deviazioni dalla formula
newtoniana e siccome non è questo il caso, la mond sarebbe già stata
falsificata. Naturalmente, non
stupisce che la mond
sia in grado di spiegare le curve di rotazione delle galassie a spirale, dal
momento che è stata costruita “su misura” per risolvere questo problema.
Tuttavia, in svariati altri casi essa si è rivelata persino superiore alla
teoria newtoniana. Noi qui ne ricordiamo un paio: la relazione di Tully-Fisher, e le galassie di bassa brillanza
superficiale. La
relazione di Tully-Fisher Questa è una relazione empirica, scoperta
nel 1977 da Brent Tully e Richard Fisher, secondo
cui la luminosità assoluta (proporzionale alla massa stellare) di una
galassia a spirale è proporzionale alla quarta potenza della velocità di
rotazione, ovvero M µ
u4.
Quest’ultima relazione viene interpretata in modo naturale dalla mond tramite
l’eq. (3), mentre nessuna spiegazione diretta è
derivabile dalla teoria newtoniana che deve necessariamente ipotizzare la
presenza di un’appropriata quantità di materia oscura opportunamente
distribuita. Galassie
di bassa brillanza superficiale Si consideri una galassia sferica di
massa M e raggio R; essa avrà una luminosità proporzionale al numero di
stelle e dunque (in assenza di materia oscura) alla massa M: L = KM, dove K è
una costante di proporzionalità nota che dipende dalle proprietà delle
stelle. A un osservatore la galassia appare come un disco luminoso di
brillanza superficiale S
= L/pR2,
indicante la quantità di radiazione proveniente dall’unità di superficie
(p.e. 1 cm2). Galassie molto estese e/o di bassa luminosità hanno
una bassa brillanza superficiale e sono indicate con l’acronimo lsb (dalle
parole inglesi Low
Surface Brightness); in caso contrario vengono dette galassie hsb (High Surface Brightness). Le
stelle nelle regioni esterne della galassia sono sottoposte, nel caso
newtoniano, ad un’accelerazione gravitazionale
Se e quando g < g0 –
ovvero quando la brillanza superficiale è minore di S0
= g0K/Gp
– le stelle esterne sono in regime mond. Possiamo allora identificare le galassie hsb come
galassie con S
> S0.
Queste galassie sono in regime misto: newtoniano nelle regioni interne e mond
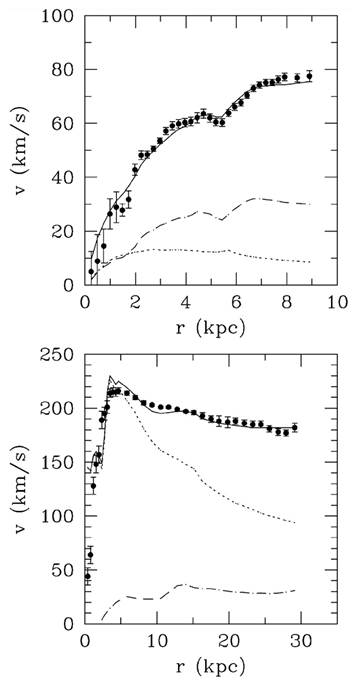
all’esterno. La curva di rotazione, dopo una ripida salita, decresce con il
raggio (come atteso dalla teoria newtoniana), fino a distanze per cui g <
g0, dove giunge al suo asintoto, restando costante (come atteso
dalla mond).
Al contrario, le galassie lsb
(S
< S0)
sono ovunque in regime mond:
in questo caso la curva di rotazione cresce fino a diventare costante (Fig. 2). Come nel caso della relazione
di Tully-Fisher, la mond spiega naturalmente le
osservazioni, mentre la teoria newtoniana deve ricorrere alla materia oscura.
Fig. 2 – Curva di rotazione della
galassia ad alta brillanza superficiale ngc2903
(pannello inferiore) e della galassia a bassa brillanza superficiale ngc1560 (pannello superiore). I
pallini neri rappresentano i dati osservativi (con relativo errore). Le linee
tratteggiate e punteggiate rappresentano, rispettivamente, il contributo
newtoniano della gravità del gas e delle stelle alla curva; come si vede, non
sono sufficienti a riprodurre i dati. La linea continua rappresenta la
previsione mond. |