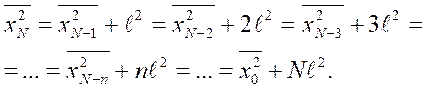|
|
|
|
|
|
|
|
|
La relazione massa-luminosità delle
stelle
Annibale
D'Ercole
Osservatorio
Astronomico - Bologna
|
La relazione tra luminosità e massa di
una stella non deriva da specifici meccanismi di evoluzione stellare, ma
riposa su tre processi fisici del tutto generali che trovano applicazione in
campi assai diversi tra loro. Essi sono: 1) la cosiddetta radiazione
di corpo nero, ovvero l’energia radiante emessa da un corpo caldo; 2)
il cammino casuale, legato a tutti i processi di diffusione, come ad esempio
quello delle molecole di zucchero in una tazza di the; 3) l’equilibrio
idrostatico, che regola la stabilità di una stella, ma anche quella
dell’atmosfera terrestre. Esaminiamo ora, singolarmente, ciascuno di questi
tre punti. 1) Un corpo caldo emette
radiazione, com’è facile verificare osservando il filamento di una lampadina
o di una stufa elettrica. Naturalmente, maggiore è la temperatura T del corpo, maggiore è la radiazione
prodotta. Consideriamo una sfera
cava (la geometria sferica non è importante, ma viene assunta per semplicità)
le cui pareti siano tenute ad una fissata temperatura. La radiazione
all’interno della sfera viene continuamente assorbita e riemessa dalle
pareti. Si può mostrare, sulla base di sole argomentazioni termodinamiche di
carattere generale, che la densità di energia radiante (ovvero l’energia di
radiazione contenuta in un centimetro cubo) dipende solo dalla temperatura e
non da altri fattori, quali la forma della cavità, il materiale della sfera,
le modalità di riscaldamento, ecc. Nel 1879 il fisico
austriaco Josef Stefan formulò la legge che porta il suo nome e che
stabilisce che la densità di energia è proporzionale alla quarta potenza
della temperatura, ovvero µ T 4. Questo significa che, se consideriamo due cavità
identiche, ma con temperature una doppia dell’altra, quella con temperatura
maggiore produrrà non 2, ma 16 (24) volte più energia. Queste
considerazioni valgono anche se la sfera è piena (e non è cava) e la
radiazione è data da fotoni che vengono continuamente assorbiti e riemessi
dagli atomi che compongono la sfera stessa (come avviene in una stella). In
conclusione, una sfera di raggio R
(e dunque volume proporzionale a R3)
e temperatura T conterrà
un’energia E proporzionale a: . (1) 2) Passiamo ora a
considerare come la radiazione prodotta al centro di una stella si propaga
fino alla superficie interagendo con il gas della stella stessa. La situazione è analoga
a quella che si verifica se lasciamo cadere una goccia di inchiostro in un
vaso pieno d’acqua: notiamo che l’inchiostro lentamente si diffonde in tutto
il volume disponibile. Ogni singola molecola di inchiostro va avanti e
indietro a causa degli urti casuali con le molecole d’acqua, ma questo non
significa che mediamente tende a rimanere nella posizione di partenza. Al
contrario, l’effetto netto è la perdita di identità della goccia e uno
“sparpagliamento” delle sue particelle a distanze sempre maggiori. Si può
dimostrare (si veda l’Appendice) che la distanza complessiva R percorsa dopo N urti casuali, separati da una distanza ℓ gli uni dagli altri,
è mediamente: . (2) Applichiamo ora questo
risultato, del tutto generale, al caso di una stella di massa M e di raggio R. I fotoni vengono generati dalle reazioni nucleari al centro
della stella. Se il gas fosse assolutamente trasparente, il tempo impiegato
da un fotone per raggiungere la superficie sarebbe τ = R/c, dove c è la velocità della luce. In
realtà, il gas risulta opaco e il fotone compie N urti con gli atomi del gas (ovvero, viene assorbito e riemesso N volte) prima di giungere in
superficie. Il tempo impiegato per fuoriuscire dalla stella è dunque τ
= Nℓ/c, dove ℓ è il cammino libero medio ovvero la distanza media tra
gli atomi. Tenendo conto dell’equazione (2), si ha τ
= R 2/ℓc. La distanza ℓ è, evidentemente,
inversamente proporzionale alla densità del gas, in quanto gli atomi sono
tanto più vicini quanto maggiore è il loro affollamento. Indicando con ρ µ
M/R 3 la densità della stella, abbiamo dunque ℓ
µ
1/ρ µ
R 3/M e possiamo finalmente scrivere: τ
µ
M/R. (3)
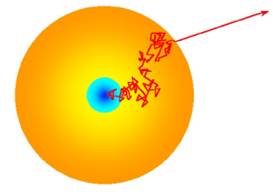
Fig. 1. Percorso
erratico di un fotone all’interno di una stella. 3) Una stella è una sfera
di gas autogravitante in equilibrio idrostatico.
Cosa significa? Un qualunque elemento di
gas della stella tende a cadere verso il centro perché attratto dalla forza
di gravità della stella stessa. D’altra parte, lo stesso elemento di gas ,
essendo caldo, tende a “evaporare via”, tende cioè a espandersi e
allontanarsi dalla stella. Queste due opposte tendenze si annullano a vicenda
e la stella rimane in equilibrio stabile. Vediamo quale relazione
deve intercorrere tra massa, raggio e temperatura stellari affinché si possa
realizzare questo equilibrio. Un elemento di gas di massa m possiede un’energia termica ET proporzionale alla
temperatura T oltre che alla sua
stessa massa (una quantità di materia doppia possiede infatti una doppia
quantità di calore): ET
µ
mT. Esso possiede anche
un’energia gravitazionale EG
che dà una misura di quanto intensamente l’elemento è legato
gravitazionalmente alla stella (in effetti l’energia gravitazionale di tale
elemento è definita come l’energia che è necessario fornire per spostarlo
all’infinito vincendo l’azione contraria della forza di gravità). Risulta
evidente che l’energia gravitazionale è tanto maggiore quanto maggiore è la
massa M della stella e/o la massa m dell’elemento perché, com’è noto,
la gravità che si esercita tra questi due oggetti è proporzionale al prodotto
mM.
Sempre in base alla legge della gravità di Newton, possiamo dire che gli
elementi di gas sono legati tanto più debolmente quanto più è grande il
raggio R della stella, poiché la
gravità diminuisce con la distanza. In conclusione, si può facilmente
dimostrare che per l’energia gravitazionale vale EG
µ
mM/R. L’equilibrio idrostatico
impone che l’energia termica e gravitazionale siano proporzionali l’una
all’altra. Dalla condizione ET
µ EG
si ottiene, pertanto: T
µ M/R. (4) Siamo ora in grado di
ricavare la relazione tra luminosità e massa di una stella di sequenza
principale. La luminosità L indica
la rapidità con cui la stella perde la sua energia di radiazione E, in altri termini L ≈ E/τ, dove τ è il tempo caratteristico di fuoriuscita della radiazione
della stella. Tenuto conto delle equazioni (1), (3) e (4) si ha: L
µ
M 3. Dunque, l’utilizzo di
argomenti del tutto generali permette di dimostrare che la luminosità di una
stella dipende, sostanzialmente, solo dalla sua massa secondo una legge di
potenza. Nonostante le
semplificazioni operate, la relazione tra luminosità e massa ottenuta è molto
simile a quella osservata L µ
M 3.5. In verità, nel
trattare la propagazione di energia attraverso la stella, abbiamo assunto che
essa avvenga per trasporto radiativo ovvero per diffusione di fotoni, come
discusso più sopra. In realtà, benché meno importante, è presente anche il
fenomeno della convezione (del tutto simile a quello che si verifica in una
pentola d’acqua che bolle) che contribuisce al trasporto di energie mediante
correnti ascensionali di gas caldo e giustifica la differenza tra il
risultato ottenuto e la relazione osservativa. Appendice: il cammino casuale Consideriamo un semplice esempio
unidimensionale. Un uomo è posizionato inizialmente nel punto xo
= 0 e si muove di volta in volta di un
passo di lunghezza ℓ verso destra o verso sinistra a seconda dell’esito
del lancio di una moneta: se, ad esempio, si realizza testa, si muove verso
destra (in direzione delle x positive), altrimenti verso sinistra
(x negative). Dal momento che le probabilità che venga
testa sono uguali a quelle che venga croce, ci si aspetta che dopo N lanci siano
avvenuti tanti spostamenti verso destra quanti verso sinistra e che, quindi,
lo spostamento medio sia nullo (`xo =
0). Questo, tuttavia, non significa che l’uomo sia rimasto in xo!
Una buona misura
dell’allontanamento dalla posizione iniziale xo
= 0 è data dal valor medio del quadrato della posizione xn
occupata dopo n lanci (il quadrato è sempre positivo e quindi la sua media
non può essere nulla). Questa posizione può essere scritta come xn
= xn-1
+ Sℓ. S = ±1
rappresenta il segno dettato dal lancio della moneta (p.e. S = 1 per testa e
S = -1 per croce): dunque si giunge in xn
dopo essersi mossi di un passo dalla posizione xn-1
raggiunta dopo n-1 lanci. Se ora facciamo il quadrato di xn
abbiamo:
Passiamo ora alla media,
tenendo conto che, ovviamente, il valor medio di S è nullo e quello del suo
quadrato vale 1 (ovvero `S = 0 e `S
2 = 1): . Questa è una relazione ricursiva, ovvero e così via. A seguito di N
successive sostituzioni possiamo allora scrivere:
In conclusione, la
distanza R percorsa dopo N passi casuali ℓ è mediamente: . |