|
|
|
|
|
|
|
|
|
L’aberrazione annua della luce
Claudio
Elidoro
|
A
chi non è mai capitato di dover fare i conti con la fretta in una giornata
piovosa? Se
non siete tra i fortunati che non sanno di cosa stia parlando, certamente
avrete ben presente che, per evitare di bagnarsi più del necessario, si è
costretti ad inclinare in avanti l’ombrello. E quanto più si allunga il
passo, tanto più l’ombrello deve essere abbassato.
Dal
punto di vista fisico la faccenda si può spiegare ricorrendo alla
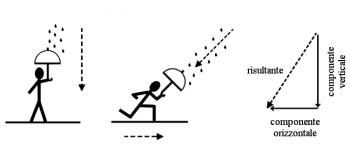
composizione del moto: le gocce d’acqua scendono verticalmente (evitiamo di
complicarci la vita con la presenza del vento) ed i malcapitati passanti si
muovono orizzontalmente. Per chi sta reggendo l’ombrello il risultato è che
le gocce di pioggia sembrano provenire da una direzione obliqua (vedi fig.
1). Una
cosa molto simile capita all’osservatore terrestre che guarda le stelle in
cielo. Anche in questo caso possiamo identificare un moto ‘verticale’ (quello
della luce che ci proviene dalle stelle) ed un moto ‘orizzontale’ (quello
della Terra che sta orbitando intorno al Sole). Dato che abbiamo a che fare
con la luce, la teoria della relatività ci dice che non possiamo applicare le
regole classiche di composizione del moto, ma questo non impedisce che, se
vogliamo osservare una stella, dobbiamo comunque inclinare il nostro
telescopio. In queste pagine considereremo solo l’approssimazione newtoniana
al problema, escludendo le ‘complicazioni’ relativistiche. La
scoperta di questo fenomeno risale al 1728. Erano gli anni in cui uno dei
problemi chiave della scienza astronomica era la determinazione delle
distanze delle stelle. Poiché il metodo impiegato era quello trigonometrico
(misura della parallasse) era indispensabile ottenere misure accuratissime
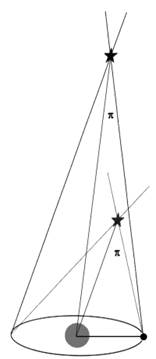
delle posizioni. Si tenga presente che l’angolo di parallasse p
è veramente piccolo, non solo assolutamente al di fuori della valutazione
dell’occhio umano, ma inaccessibile anche ai migliori telescopi dell’epoca
(fig. 2). Il fatto che non si riuscisse per nessuna stella a individuare la
parallasse era un’ottima carta in mano ai detrattori della teoria
Copernicana, la prova tangibile dell’immobilità della Terra nel cosmo. Il
problema di fondo, però, e lo stesso Galilei lo aveva intuito, era che si
doveva rilevare un angolo veramente esiguo. Un esempio numerico può aiutare a
comprendere la situazione. La stella con parallasse p
più grande è quella più vicina a noi. Si tratta di a Centauri, un astro situato a poco più di 4
anni luce dal Sole. Ebbene, la parallasse di questa stella è solamente di
0,760 secondi d’arco, una vera inezia.
Per
i sostenitori della teoria eliocentrica, dunque, diventava di fondamentale
importanza dimostrare che la misura della parallasse non era un’utopia. Tra
gli scienziati impegnati in questa impresa vi era anche l’inglese James
Bradley, professore ad Oxford ed astronomo all’Osservatorio di Greenwich. Le
sue osservazioni si erano concentrate su g Draconis,
nota anche con il nome arabo di Al Ras
al tannin (“la testa del drago”) o, più
semplicemente, Eltanin. Analizzando le sue
misurazioni, Bradley si accorse che nel corso dell’anno la posizione di
quella stella era caratterizzata da un continuo spostamento fino ad un
massimo di 20,5 secondi d’arco. Il modo in cui variava la posizione della
stella nel corso dell’anno sembrava contraddire quanto previsto dalla
geometria della parallasse. Si
trattava dunque di scoprirne la causa. Scartata l’ipotesi che quella
variazione nella posizione apparente di g Draconis
fosse dovuta ad effetto di parallasse, l’idea iniziale di Bradley fu la
presenza di errori strumentali, suggerita anche dal fatto che quello strano
spostamento si mostrava comune ad altre stelle. Verificata con meticolosità
l’affidabilità della strumentazione impiegata, l’astronomo inglese ebbe
l’intuizione giusta: quello che si stava osservando era il risultato della
composizione del moto della luce proveniente dalle stelle con il moto della Terra
intorno al Sole. Servita su un vassoio d’argento, l’astronomia del XVIII
secolo aveva a disposizione una inaspettata e schiacciante prova della
correttezza delle idee copernicane. Il
fenomeno scoperto da Bradley è conosciuto con il nome di aberrazione annua della luce
e, ancora oggi, costituisce una delle prove fondamentali e dirette della
rivoluzione terrestre intorno al Sole. Il termine aberrazione deriva dal
titolo del libro dell’astronomo bolognese Eustachio Manfredi ‑ De
annuis inerrantium stellarum aberrationibus ‑ che per
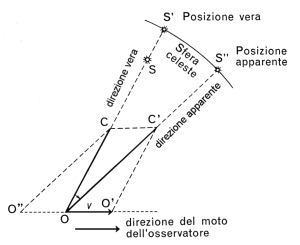
primo confermò con le osservazioni di 90 stelle l’ipotesi di Bradley. Facciamo
riferimento alla fig. 3 per chiarire meglio il fenomeno.
Se
l’osservatore in O fosse immobile, vedrebbe la stella S proiettata sulla
volta celeste nel punto S’ (direzione
vera). Il raggio luminoso, infatti, seguirebbe il percorso SO. Ma
l’osservatore si sta muovendo e, nel tempo impiegato dalla luce a percorrere
il tratto dalla stella in S’ ad O, si è spostato in O’. Questo significa che
il telescopio non è più puntato lungo la direzione OC, bensì lungo O’C’ e in
conseguenza di ciò l’osservatore non può vedere la stella. Per rimediare a
questo fatto lo strumento dovrebbe essere disposto lungo la retta O”C. Questo
fa sì che, mentre la luce percorre il tratto da S’ ad O, l’osservatore si
sposta da O” in O e può così intercettare il raggio luminoso della stella. In
pratica, però, l’allineamento del telescopio risulta essere inclinato verso
la direzione del moto e la stella viene “vista” sulla volta celeste come se
fosse nel punto S” (direzione apparente).
L’angolo COC’ rappresenta dunque la deviazione apparente della posizione
della stella dovuta all’aberrazione della luce ed è dunque chiamato angolo di aberrazione. La
sua ampiezza dipende dalle due velocità in gioco, quella della luce e quella
della Terra. Poiché l’oscillazione annuale individuata da Bradley è
strettamente legata al moto orbitale della Terra, risente anche del fatto che
nel corso dell’anno la direzione di questo moto cambia. Questo comporta che
la posizione osservata di una stella descriva un’ellisse intorno alla sua
posizione vera. Le
ellissi di aberrazione, inoltre, sono sempre più schiacciate man mano che si
osservano delle stelle più lontane dal polo dell’orbita terrestre, fino a
diventare semplici segmenti nel caso di stelle poste sul piano dell’orbita
(piano dell’eclittica). Il
valore di 20,50 secondi d’arco trovato da Bradley per l’angolo di aberrazione
è facilmente verificabile risolvendo trigonometricamente un triangolo
rettangolo i cui cateti sono, rispettivamente, la velocità della luce e la
velocità di rivoluzione della Terra (si vedano a questo proposito i calcoli
proposti nell’approfondimento). Giunti
al termine di questa esposizione è doveroso ricordare ancora che sono stati
evitati calcoli relativistici. Inoltre, sottolineiamo che si è accennato
unicamente alle conseguenze del moto di rivoluzione intorno al Sole
(aberrazione annua della luce), esistendo anche una aberrazione diurna
dovuta al moto di rotazione terrestre, ma di dimensioni molto inferiori ed
un’ulteriore aberrazione, detta sistematica; originata dal moto del
Sistema solare. È quindi evidente che per una trattazione più rigorosa
sarebbe necessario mettere in conto anche gli altri movimenti compiuti dal
nostro pianeta nonché le regole di composizione delle velocità previste dalla
relatività.
|