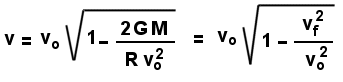
dove 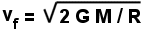  è detta velocità di fuga.
Se v_o=v_f  (ovvero T_o=U ) il proiettile riesce a stento ad allontanarsi e la sua velocità diminuisce fino ad annullarsi a grande distanza.
Per v_o<v_f  il radicando diventa negativo e non è possibile eseguire l’operazione di radice; dal punto di vista fisico, questo significa che il proiettile non riesce ad allontanarsi indefinitamente ed è destinato ad invertire il suo moto e ricadere a terra. Dunque, per permettere ad un qualunque oggetto di abbandonare il corpo a cui è legato gravitazionalmente bisogna dotarlo di una velocità almeno pari a quella di fuga.
Si noti che v_f  non dipende dalla massa del proiettile ma solo dalle caratteristiche del corpo celeste.
Per un corpo sufficientemente massiccio e compatto la velocità di fuga può arrivare ad essere pari o superiore alla velocità della luce c. Dall’espressione per la velocità di fuga si ricava che in questo caso il raggio dell’astro deve essere inferiore o uguale al raggio di Schwarzschild R_S=2GM/c².
Un corpo del genere è detto buco nero in quanto neanche la luce eventualmente prodotta alla sua superficie è in grado di allontanarsi e raggiungere, ad esempio, un osservatore lontano: un buco nero risulta pertanto invisibile. Dal momento che nulla può superare la velocità della luce, qualunque cosa cada all’interno del raggio di Schwarzschild non può più tornare indietro e scompare per sempre dalla vista di un osservatore esterno.

Vediamo ora l’effetto del buco nero sullo scorrere del tempo.
Ad un fotone di frequenza  è associata un’energia elettromagnetica E=h , dove h è la costante di Planck. Tramite la nota relazione relativistica E=mc² che lega l’energia alla massa di una particella, possiamo formalmente attribuire ad un fotone una massa m_v=E/c²=h/c² .
Pertanto, contrariamente a quanto stabilito nella fisica classica, i fotoni risentono di un’eventuale forza di gravità che agisca su di essi. Così come un oggetto materiale perde progressivamente energia cinetica diminuendo la propria velocità man mano che si allontana dal corpo che lo attrae, analogamente un fotone perde energia riducendo la propria frequenza.
Dunque l’energia di un fotone sfuggito all’astro che lo ha emesso non è uguale a quella iniziale E_o giacché in parte è stata spesa per controbilanciare l’energia di legame: l’effettiva energia del fotone è data da E=E_o-U.
Questa condizione sull’energia porta alla relazione tra la frequenza _o al momento dell’emissione e la frequenza  misurata da un ipotetico osservatore distante:

Questa espressione, ottenuta con semplici passaggi algebrici, rappresenta una buona approssimazione nel caso di astri "normali" con raggi assai superiori al raggio di Schwarzschild e campi gravitazionali deboli (R_S/R<<1). Nei pressi di un buco nero, dove la gravità è consistente e R_S/R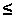1, si deve ricorrere alla relazione esatta che si ottiene dalla teoria della relatività generale e che vale (vedi nota a piè pagina)

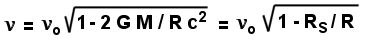
Questa formula è simile a quella ottenuta per la velocità di un corpo materiale e valgono considerazioni analoghe. La frequenza della radiazione emessa da astri con R>R_S diminuisce, e questo effetto è detto spostamento verso il rosso gravitazionale (per il fatto che la radiazione rossa è quella di minore frequenza osservabile dall’occhio umano).
Per R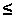R_S la frequenza si annulla, ovvero il fotone non è in grado di abbandonare la regione da cui è stato emesso. Abbiamo dunque riottenuto il significato di raggio di Schwarzschild seguendo un ragionamento diverso dal precedente.
Tuttavia questo ragionamento è in grado di portarci più lontano.
La frequenza di un fotone è uguale alla frequenza con cui oscillano gli elettroni dell’atomo da cui è stato emesso. Queste oscillazioni, al pari di quelle di un pendolo, scandiscono il tempo che passa. Abbiamo visto che per un osservatore lontano la frequenza della radiazione emessa da atomi posti vicino al raggio di Schwarzschild appare diminuire; questo equivale a dire che per tale osservatore il tempo nei pressi di un buco nero rallenta. Questo rallentamento aumenta man mano che ci si avvicina al buco nero: al raggio di Schwarzschild la gravità è così forte che il tempo "si ferma".
Durante la caduta di un’astronave verso un buco nero il tempo continua a scorrere normalmente per lo sfortunato occupante. All’osservatore distante, a causa della distorsione temporale, l’astronave sembra invece rallentare sempre più man mano che si avvicina ad una distanza pari al raggio di Schwarzschild, senza raggiungerla mai; contemporaneamente i fotoni che giungono dall’astronave sono sempre meno energetici, e l’immagine progressivamente "sbiadisce" fino a scomparire.

Nota

E' facile vedere che la formula esatta e quella approssimata danno lo stesso risultato nel caso di campi gravitazionali deboli.
Posto y=v/v_o  e x=R_s/ R  le formule esatta e approssimata si scrivono, rispettivamente  y=(1-x)^1/2   e  y=1-0.5x.
Elevando al quadrato entrambe le espressioni otteniamo, nell'ordine, y²=1-x e y²=1-x+0.25x².
Avendo assunto x<<1, il termine quadratico dell'ultima espressione può essere trascurato; di conseguenza in entrambi i casi si ottiene y=(1-x)^1/2.