|
|
|
|
|
|
|
|
|
Le distanze
dei pianeti
Claudio
Elidoro
|
C'è qualche
regola che governa le distanze dei pianeti dal Sole? La
domanda è molto semplice, ma non altrettanto lo è la risposta – sempre
ammesso che esista una risposta chiara. Come molti altri temi astronomici,
anche il problema delle distanze planetarie non è un affare recente. L’idea
che ci fosse una legge matematica a governare ogni moto celeste – e di
riflesso le distanze planetarie – si perde nella notte dei tempi, sostenuta
da un lato dal pensiero filosofico che voleva la Natura espressione somma
dell’ordine e dall’altro da quello religioso che non poteva concepire l’opera
di un Creatore se non in termini di assoluta e rigorosa precisione. I
Pitagorici, per esempio, sostenevano che la distanza tra due pianeti
successivi fosse costante e ritenevano che tale costante fosse uguale a 3. Lo
stesso Keplero (1571-1630) si diede molto da fare per ideare un sistema di
orbite planetarie fondato sulla regolarità e sulla perfezione matematica. Nel
suo Mysterium Cosmographicum,
pubblicato nel 1595, propone un continuo alternarsi di sfere (corrispondenti
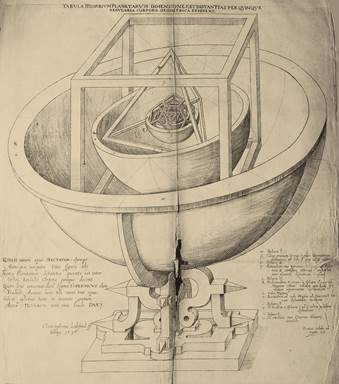
alle orbite planetarie) e di solidi regolari inscritti in esse (Fig. 1).
Fig.
1. La costruzione geometrica di Keplero. Sulla sfera più
esterna si colloca l’orbita di Saturno. Inscritto in essa, Keplero colloca un
cubo il quale, a sua volta, racchiude la sfera dell’orbita di Giove.
Continuando in questa successione di solidi, all’interno della sfera di Giove
– che la separa da quella di Marte – viene collocato un tetraedro; tra Marte
e la Terra il solido prescelto è il dodecaedro, tra la Terra e Venere
l’icosaedro ed infine, tra Venere e Mercurio, l’ottaedro. Qualche
semplice calcolo può portarci a vedere come questa costruzione, notevole dal
punto di vista geometrico, sia scarsamente rispondente ai dati reali. Il
fatto, però, che anche il grande Keplero si occupasse attivamente del
problema delle distanze planetarie la dice lunga su quanto tale problema
fosse diffuso e studiato. Quando,
oltre alle idee filosofiche, si poté contare anche su valori numerici
attendibili, la caccia a una regola matematica cominciò a farsi più serrata.
In uno scritto del 1730, Christian Freiherr von
Wolff (1679-1754) osservava: Se poniamo a 10 la distanza tra la Terra e il Sole, allora
la distanza di Mercurio dal Sole è 4, quella di Venere 7, quella di Marte 15,
quella di Giove 52 e quella di Saturno 95. Non
siamo di fronte all'annuncio di una regola matematica e neppure a una precisa
successione numerica, ma si apre la strada a quella che per alcuni secoli
sarà una risposta chiave alla domanda sulla regolarità delle orbite
planetarie: la cosiddetta “legge di Titius e Bode”
(che “legge” non è, bensì relazione empirica). Questa famosa relazione fece
la sua prima apparizione nel 1766 quando Johann Daniel Titius
von Wittenberg (1729-1796), traducendo in tedesco il libro del filosofo e
naturalista svizzero Charles Bonnet dal titolo Contemplation de la Nature (un autentico best
seller dell'epoca), inserì la seguente annotazione: Se poniamo la distanza di Saturno dal Sole uguale a 100
unità, allora Mercurio è distante dal Sole 4 di queste unità; Venere 4 + 3 =
7 medesime unità; la Terra 4 + 6 = 10; Marte 4 + 12 = 16. Vediamo però che
tra Marte e Giove questa esatta progressione si interrompe. A Marte dovrebbe
succedere la posizione di 4 + 24 = 28 di queste unità, ma fino ad ora non è
stato trovato né un pianeta principale né un satellite. Che il Creatore abbia
lasciato questa posizione vuota? Giammai! [...] Più in là di questo, non
ancora scoperto, si colloca la posizione di Giove di 4 + 48 = 52; e quella di
Saturno a 4 + 96 = 100 unità. Davvero una lodevole relazione. Esisteva,
dunque, una logica matematica nella sequenza delle distanze planetarie. A
dispetto della semplicità, la relazione di Titius
non ebbe comunque molto successo. Da quando, però, nel 1772 Johan Elert Bode (1747-1822) – astronomo tedesco di grande fama
– inserì l’osservazione di Titius nella seconda
edizione del suo diffusissimo libro di astronomia (senza per altro dare il
dovuto credito all’autore) la «lodevole relazione» conobbe un incredibile
successo. Allorquando
le sue previsioni si dimostrarono corrette anche per Urano (scoperto da
Herschel nel 1781) e per gli asteroidi (Piazzi scoprì Cerere nel 1801), venne
considerata un autentico caposaldo dell’astronomia. Era secondario che la
successione fosse costruita anche con un valore infinito (nel caso di
Mercurio), che nella successione si potessero ipotizzare infiniti valori
prima di quello corrispondente a Venere, che in corrispondenza dell’indice 3
vi fosse una anomala coesistenza di tanti corpi celesti (gli asteroidi) e che
mancasse una esauriente spiegazione fisica: la relazione funzionava
egregiamente e tanto bastava. Il
declino cominciò nel 1846, quando Johan Gottfried Galle, seguendo le
indicazioni di Adams e Leverrier, individuò il
pianeta Nettuno. Secondo la successione la distanza avrebbe dovuto essere di
38,8 unità astronomiche (ua)
ma l’orbita di Nettuno si rivelò di oltre 8 ua più vicina al Sole. Le perplessità
presero infine l'aspetto di sonora bocciatura ottantaquattro anni più tardi,
allorché Clyde Thombaugh scoprì Plutone e tutti si
accorsero che le 77,2 ua
previste dalla successione erano quasi il doppio della reale distanza alla
quale l'oggetto orbitava. Ci furono molti tentativi di revisione della
formulazione matematica, sia per far corrispondere in modo più accurato le
sue previsioni ai dati reali, sia per eliminarne le incongruenze matematiche,
ma c'era sempre qualcosa che non quadrava mai del tutto. Destinata
all'oblio? Non proprio. In tempi recenti, infatti, si è provato a verificare
l'esistenza di una relazione analoga per uno dei sistemi planetari
extrasolari più affollati scoperti finora, quello di 55 Cancri. Nel 2008 i
due astronomi messicani Arcadio Poveda e Patricia
Lara hanno proposto per quel sistema planetario una formulazione della legge
di tipo esponenziale con risultati, a loro dire, davvero notevoli. Non solo
le distanze dei cinque pianeti di 55 Cancri sono tutte correttamente descritte
dalla relazione, ma la presenza di due “orbitali” ai quali non corrisponde
nessun oggetto planetario li spinge a ipotizzare l'esistenza di due pianeti
non ancora scoperti. Si ripeterebbe, insomma, la storia di Urano e Cerere. Non
tutti concordano con il lavoro di Poveda e Lara, ma
è davvero curioso che, a quasi due secoli e mezzo dalla sua prima
formulazione, la «lodevole relazione» di Titius e
Bode sia ancora sulla cresta dell'onda. |