 Supponiamo
che dal corpo centrale di una sorgente venga emesso un getto di gas verso
l’osservatore lungo una direzione che forma un angolo Supponiamo
che dal corpo centrale di una sorgente venga emesso un getto di gas verso
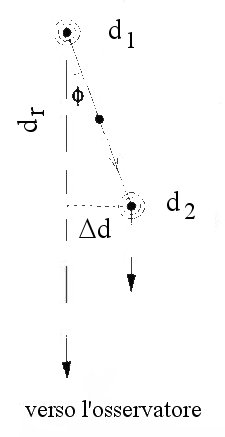
l’osservatore lungo una direzione che forma un angolo  con la linea di vista (si veda la figura). Supponiamo inoltre che il getto
si muova con una velocità v vicina alla velocità
della luce c .
con la linea di vista (si veda la figura). Supponiamo inoltre che il getto
si muova con una velocità v vicina alla velocità
della luce c .
Siano d1
e d2=d1+v t
le distanze dalla sorgente centrale a cui si trova il getto ai tempi t1
e t2=t1+ t
le distanze dalla sorgente centrale a cui si trova il getto ai tempi t1
e t2=t1+ t,
rispettivamente. t,
rispettivamente.
Nel passare da d1
a d2 il getto si avvicina all’osservatore
di una quantità dr=vcos  t
, mentre la luce emessa in direzione dell’osservatore quando era in d1
ha compiuto nel frattempo un tratto c t
, mentre la luce emessa in direzione dell’osservatore quando era in d1
ha compiuto nel frattempo un tratto c t
. Dunque, definendo per comodità la variabile t
. Dunque, definendo per comodità la variabile 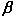 =v/c
, i due impulsi luminosi, quello emesso in d1
e quello emesso in d2, viaggiano verso l’osservatore
ad una distanza =v/c
, i due impulsi luminosi, quello emesso in d1
e quello emesso in d2, viaggiano verso l’osservatore
ad una distanza
 dr
= c (1- dr
= c (1-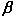 cos cos ) ) t
l’uno dall’altro, e giungono distanziati da un tempo t
l’uno dall’altro, e giungono distanziati da un tempo
 t'
= t'
=  dr / c = (1- dr / c = (1-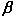 cos
cos ) ) t
. t
.
Lo spostamento compiuto dal getto
in direzione ortogonale alla linea di vista (ovvero lo spostamento sulla
sfera celeste, che è quello effettivamente misurato dagli astronomi)
nel passaggio da d1 a d2
è dato da
 d
= v sen d
= v sen   t
. t
.
Dunque per l’osservatore la velocità
del getto in questa direzione è pari a
v' =  d
/ d
/  t' ,
ovvero v' = c ( t' ,
ovvero v' = c (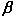 sen sen  )
/ (1- )
/ (1-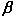 cos cos ). ).
Se
il getto si muove lungo una direzione ortogonale alla linea di vista, si
ha
 = =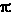 /2,
sen /2,
sen =1 , cos =1 , cos =0
e v' = v. =0
e v' = v.
La velocità osservata è
effettivamente quella con cui si sposta il getto. Ma per un getto che si
muova verso l’osservatore ( <<1)
la velocità apparente può superare quella della luce. <<1)
la velocità apparente può superare quella della luce.
Si può infatti dimostrare che
per il particolare valore  m
dell’angolo, tale per cui cos m
dell’angolo, tale per cui cos m
= m
= 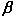 , si ottiene il
valore massimo per la velocità apparente , si ottiene il
valore massimo per la velocità apparente
v'm = c 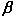 / (1-
/ (1-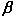 2)1/2
, superiore alla velocità della luce per valori di 2)1/2
, superiore alla velocità della luce per valori di 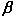 vicini all’unità, ossia nel caso di velocità v
del getto vicina a quella della luce.
vicini all’unità, ossia nel caso di velocità v
del getto vicina a quella della luce.
|
 Supponiamo
che dal corpo centrale di una sorgente venga emesso un getto di gas verso
l’osservatore lungo una direzione che forma un angolo
Supponiamo
che dal corpo centrale di una sorgente venga emesso un getto di gas verso
l’osservatore lungo una direzione che forma un angolo