|
|
|
|
|
|
|
|
|
Il principio di Mach
Annibale
D’ercole
|
Nel 1851 Jean-Bernard-Leon Foucault,
tramite un pendolo appeso alla cupola del Pantheon di Parigi, dimostrò che la
Terra gira rispetto alla volta celeste e non il contrario, come appare
osservando il cielo stellato, e come si era generalmente creduto fino ad
allora. La dimostrazione di Foucault si basava sulla fisica newtoniana e sul
concetto di spazio assoluto in essa contenuto. Supponiamo, per
semplicità, di porre un pendolo al polo nord. Su di esso agisce solo la forza
di gravità, che è diretta verticalmente e contenuta nel piano di oscillazione.
Di conseguenza, ad un osservatore collocato sopra al polo e non rotante con
la Terra, l’orientamento di tale piano risulta fisso perché non vi sono forze
ortogonali ad esso che possano farlo ruotare. Rispetto al piano di
oscillazione la Terra ruota in senso antiorario compiendo un giro in 24 ore.
(Fig. 1)
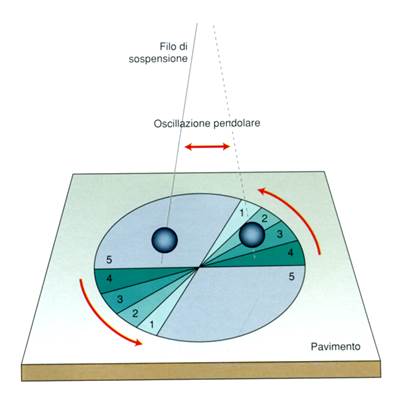
Fig. 1. Un
pendolo (che per semplicità immaginiamo posto al polo nord) oscilla sempre
nello stesso piano (quello della pagina) mentre sotto di lui la Terra ruota
in senso antiorario (la rotazione terrestre è indicata dalle frecce rosse).
Se il pendolo sfiorasse il pavimento sottostante cosparso di sabbia,
traccerebbe solchi sempre diversi, ruotati progressivamente in senso orario
(indicati dalla numerazione progressiva). Pertanto, ad un osservatore posto
sulla Terra, fermo rispetto al pavimento, il piano di oscillazione appare
precedere in senso orario. A un osservatore posto
sulla Terra, invece, la Terra stessa appare ferma, mentre è il piano di
oscillazione del pendolo a ruotare – a precedere – in senso orario compiendo
360 gradi nell’arco di 24 ore. (La situazione è più complicata per altre
latitudini. All’equatore il pendolo non precede affatto, mentre a latitudini
intermedie il periodo di precessione ha valori intermedi.) Questo osservatore
attribuisce la precessione alla forza di Coriolis,
una forza inerziale che, assieme alla forza centrifuga (inessenziale in
questo esempio), compare nei sistemi rotanti e che, essendo ortogonale al
piano di oscillazione del pendolo, ne determina la rotazione. (La forza di Coriolis appare nei sistemi rotanti e si esercita sui
corpi in movimento. Per avere una idea, sia pure semplificata, di come agisce
tale forza, si consideri un treno che si muova verso sud lungo un’ipotetica
ferrovia che congiunge il polo nord all’equatore, seguendo un determinato
meridiano. Un osservatore posto sopra al polo nord e che non partecipa alla
rotazione terrestre osserva il treno muoversi sui binari verso sud; ma i
binari ruotano con la Terra e “spingono” il treno lateralmente verso est, per
farlo partecipe di questa rotazione. In assenza di questo intervento, il
treno, a causa della sua inerzia, proseguirebbe in avanti lungo la sua
traiettoria originaria e i binari si allontanerebbero verso est. Un
osservatore sulla Terra registra la spinta laterale verso est operata sul
treno dai binari e la interpreta come reazione a una spinta laterale opposta
– verso ovest – dovuta appunto alla forza di Coriolis.
Nel caso di un treno in moto verso il polo nord, la forza di Coriolis sarebbe diretta verso est. Questa forza
influenza i moti su larga scala nell’atmosfera ed è responsabile della
circolazione delle maggiori correnti oceaniche, che è oraria nell’emisfero
nord ed antioraria in quello sud.) Secondo la fisica
newtoniana, dunque, l’orientamento del piano di oscillazione del pendolo
rimane effettivamente inalterato nello spazio assoluto ed è la Terra a
ruotare “veramente”; a riprova del moto accelerato della Terra rispetto allo
spazio assoluto vi è proprio l’insorgere della forza inerziale di Coriolis, che è invece assente nel sistema di riferimento
in quiete rispetto al piano del pendolo (in cui si trova l’osservatore al di
sopra del polo nord). Come abbiamo visto nel
livello base, questa interpretazione fu contestata da Mach. Se rimuovessimo
dall’universo tutta la materia, ad eccezione della Terra, come potremmo
sapere se la Terra sta girando o meno? E come farebbe il pendolo a “sapere”
se precedere o no? Osservativamente si
trova che la forza di Coriolis insorge nei sistemi
di riferimento in cui la volta celeste appare ruotare sopra la nostra testa e
scompare in quelli in cui le stelle distanti appaiono fisse. Mach considerò
questa coincidenza non casuale e ritenne che l’esperienza di Foucault non
evidenziasse la rotazione “assoluta” della Terra, ma solo la sua rotazione
rispetto alle stelle fisse; se la Terra fosse ferma e fosse la volta celeste
a ruotare, nulla cambierebbe nel comportamento del pendolo di Foucault. Sono
dunque le stelle fisse a determinare l’inerzia del pendolo, responsabile
della sua precessione, tramite una qualche interazione sconosciuta. Per chiarire meglio
quest’ultimo punto, si consideri un singolo pianeta in un universo
completamente vuoto. Per quanto detto più sopra, non ha senso per Mach in
questo caso parlare di rotazione. Il piano di oscillazione di un pendolo di
Foucault, posto su questo pianeta solitario, non potrebbe dunque mai
precedere. Se il pendolo sfiorasse uno strato di sabbia sparsa sul pavimento
sottostante, traccerebbe sempre lo stesso solco. Immaginiamo ora di
aggiungere un po’ di materia nelle regioni distanti dell’universo. In questo
caso diventerà possibile osservare un’eventuale rotazione del pianeta
rispetto alla materia distante. Tuttavia, se questa materia fosse scarsa,
l’influenza di quest’ultima sull’inerzia del pendolo rimarrebbe trascurabile
e così pure la forza di Coriolis che da questa
inerzia dipende. Il pendolo, dunque, continuerebbe sostanzialmente a
tracciare sempre lo stesso solco sulla sabbia, in assenza di una forza
consistente che causi la precessione del piano di oscillazione. Questa
precessione diverrebbe sempre più apprezzabile all’aumentare della materia
posta nell’universo, fino ad acquistare un periodo pari a quello di rotazione
del pianeta rispetto alle stelle fisse. Il pendolo traccerebbe allora solchi
sulla sabbia la cui direzione cambia al passare del tempo con un periodo pari
a quello della rotazione relativa tra pianeta e stelle fisse. Gli argomenti
precedenti, del tutto qualitativi, furono riconsiderati in maniera assai più
rigorosa e quantitativa da Einstein che fu fortemente influenzato dalle idee
di Mach nel formulare la teoria della relatività generale. Questa teoria
afferma che l’azione gravitazionale di un oggetto, quale ad esempio un
pianeta, consiste nel curvare lo spazio intorno a sé. Come abbiamo accennato
nel livello base, questo permette di capire come la materia distante possa
determinare istantaneamente l’inerzia degli oggetti. Vi è un’ulteriore azione
esercitata sullo spazio circostante dall’oggetto gravitante nell’eventualità
che esso ruoti. In questo caso, infatti, esso “trascina” con sé lo spazio
(più precisamente, lo spazio-tempo). Questo fenomeno è simile a quello di una
sfera rotante all’interno di un contenitore di un fluido viscoso, quale cioccolata
liquida o miele: la sfera comunica un moto rotatorio al fluido nelle sue
vicinanze e un eventuale oggetto presente nel fluido, ad esempio un chicco di
caffè, pur rimanendo fermo rispetto al fluido locale, viene posto in orbita
attorno all’oggetto centrale a causa dell’effetto di trascinamento. Questo
aspetto fu studiato in particolare da Josef Lense e
Hans Thirring nel 1918, poco dopo la pubblicazione
da parte di Einstein della Teoria della Relatività Generale. I due fisici
considerarono un guscio sferico di massa M e raggio R, ruotante su se stesso
con velocità angolare w in
un universo altrimenti vuoto. Risolvendo le complicate equazioni
relativistiche, Lense e Thirring
dimostrarono che sia lo spazio interno che quello esterno al guscio tendono
ad essere trascinati dal guscio stesso, con un efficacia che aumenta
all’aumentare di M (e al diminuire di R). Fissiamo ora l’attenzione
all’interno del guscio, e immaginiamo che nel centro sia posto un pianeta al
cui polo nord (individuato, assieme al polo sud, dall’asse di rotazione del
guscio che attraversa il pianeta) oscilli un pendolo. Nel caso che il pianeta
e il guscio siano fermi (l’uno rispetto all’altro), il piano di oscillazione
del pendolo rimarrà ovviamente invariato rispetto ad entrambi. Se però il
guscio comincia a ruotare rispetto al pianeta (o viceversa), lo spazio, e in
particolare il piano di oscillazione, si mette anch’esso in rotazione
rispetto al pianeta con una velocità angolare W
data da
dove G è la costante di
gravitazionale, c la velocità della luce, e k è una costante dell’ordine
dell’unità. All’aumentare di M, W
cresce sempre più, fino ad arrivare ad W = w
per
In questo caso, dunque,
il piano di oscillazione del pendolo rimane “agganciato” al guscio, ovvero
resta fermo rispetto ad esso e precede rispetto al pianeta, come suggerito da
Mach. Tornando a considerare
la Terra in luogo del pianeta centrale e la materia distante al posto del
guscio di materia, dobbiamo sottolineare che in realtà il pendolo “vede” non
solo le stelle fisse, ma anche la Terra stessa; quest’ultima, benché di massa
trascurabile rispetto al resto dell’universo, è però assai più vicina e
dunque esercita un effetto piccolo, ma non nullo. Pertanto, il piano di
oscillazione del pendolo deve raggiungere una sorta di compromesso tra il
seguire le stelle distanti e il rimanere agganciato alla Terra: le stelle
distanti hanno una sostanziale prevalenza, ma il piano di oscillazione accumula
un lieve ritardo rispetto ad esse a causa dell’influenza frenante della
Terra. In un anno il ritardo accumulato è molto piccolo, pari a 39
millisecondi, l’equivalente dello spessore di un capello visto da una
distanza di 400 metri! (L’esiguità del trascinamento spaziale dovuto alla
rotazione della Terra è conseguenza della scarsa gravità esercitata da
quest’ultima. Al contrario, si ritiene che l’effetto Lense-Thirring
nei pressi di un buco nero rotante sia enorme e che possa essere responsabile
dell’origine dei potentissimi jet che si osservano nei quasar distanti.) Nonostante la sua
estrema piccolezza, è stato possibile misurare questa precessione tramite il Gravity Probe B, un satellite posto in orbita polare
attorno alla Terra. Secondo la fisica newtoniana, in assenza di altre forze
agenti sul satellite oltre a quella gravitazionale, il piano dell’orbita
mantiene il proprio orientamento, indipendentemente dal fatto che la Terra
ruoti o no. In base alla relatività generale, invece, l’effetto Lense-Thirring prevede, come s’è detto, un trascinamento
del piano orbitale che precede nella stessa direzione della rotazione
terrestre. Dopo 48 anni spesi per lo studio e la realizzazione
dell’esperimento, lo scorso maggio il satellite Gravity
Probe B ha effettivamente verificato questa precessione. (Fig. 2)
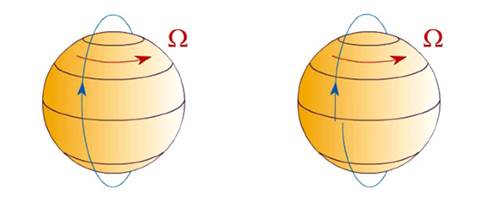
Fig. 2. Rappresentazione schematica dell’esperimento Gravity Probe B. Un satellite in orbita polare attorno alla
Terra dovrebbe continuare ad orbitare sempre sullo stesso piano,
indipendentemente dal fatto che il nostro pianeta ruoti con velocità angolare
W (figura a sinistra). Secondo la relatività generale,
invece, la Terra trascina nella sua rotazione lo spazio circostante e il
piano orbitale del satellite ruota, sia pure minimamente (figura a destra). Nonostante questa
straordinaria conferma sperimentale, l’effetto Lense-Thirring
non prova che il principio di Mach sia effettivamente inglobato – e dunque
“spiegato” – dalla teoria della relatività. Una disamina di questo punto è al
di là dei limiti di questi appunti; qui basterà notare che, parlando di
guscio in rotazione, Lense e Thirring
riferiscono tale rotazione rispetto allo spazio distante assunto “fermo”,
restaurando in qualche modo il concetto di spazio assoluto. (A beneficio del
lettore che abbia una sia pure minima “infarinatura” dei concetti base della
relatività generale, aggiungiamo che, se nello spazio distante fosse presente
della massa, il principio di Mach verrebbe ovviamente recuperato. Tuttavia,
questa massa avrebbe l’effetto di curvare e chiudere lo spazio su larga
scala. Di conseguenza, è possibile trovare soluzioni machiane
delle equazioni relativistiche solo in casi particolari in cui lo spazio a
grande distanza è assunto chiuso, condizione rappresentata schematicamente
dall’eq. (1). A titolo di esempio, per k = 2,
questa equazione indica la chiusura dello spazio attorno a un buco nero di Schwarzschild (nulla può sfuggire al di là di R = 2GM/c2))
Lo stesso Einstein dovette ammettere, non senza una certa riluttanza, che
occorreva partire dall'ipotesi che lo spazio sia assoluto e quindi debba
possedere una sua propria struttura, anche in assenza di materia. Di conseguenza, il
problema dell’origine dell’inerzia (e delle forze fittizie ad essa connesse)
rimane ancora scarsamente compreso. |