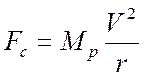La materia oscura nelle galassie a spirale
Annibale D'Ercole
Osservatorio Astronomico - Bologna

È ben noto che i pianeti ruotano attorno al Sole seguendo le tre leggi di Keplero. Fu anche grazie a queste leggi che Newton riuscì a descrivere la forza di gravità secondo la nota formula

        (1)

 

In questa formula, G rappresenta la costante di gravità, Ms e Mp indicano, rispettivamente, la massa del Sole e di un pianeta ed r la loro distanza. Il segno negativo sta a indicare la direzione centripeta della forza.

Benché l’orbita reale dei pianeti sia di forma ellittica, in quel che segue assumeremo, per semplicità, che le orbite planetarie siano circolari (l’orbita della Terra, per esempio, è solo debolmente ellittica). Dal momento che i pianeti hanno masse enormemente più piccole di quella del Sole, quest’ultimo è praticamente fermo e il suo centro coincide con il centro dell’orbita planetaria. L’orbita del pianeta è stabile, esso cioè continua a percorrere da miliardi di anni sempre la stessa traiettoria, senza cadere verso il Sole, nonostante l’attrazione di quest’ultimo. Questo è possibile grazie all’azione della forza centrifuga che insorge a causa della rivoluzione del pianeta attorno al Sole. In effetti, un pianeta che si muove con velocità V “si sente” sottoposto a due forze: la forza centripeta del Sole e quella centrifuga

.              (2)

 

Dunque, per rimanere sempre alla stessa distanza dal Sole, bisogna che le due forze si equivalgano e che il risultato netto sia nullo, ovvero Fg = -Fc (il segno negativo è dovuto al fatto che le due forze puntano in direzioni opposte). Da quest’ultima uguaglianza e dalle equazioni (1) e (2), si ottiene V = K/r ½, dove K = (GMs )½ è una costante. Pertanto, ci si aspetta che i pianeti più distanti siano più lenti (orbita kepleriana) e in effetti questo è proprio quello che si osserva.

La struttura della Via Lattea è grosso modo data da una sfera centrale (il “bulge”) e da un disco sottile più esteso. Le stelle sul disco ruotano attorno al centro del bulge che coincide con quello del disco. La curva di rotazione, ovvero l’andamento della velocità orbitale delle stelle a seconda della loro distanza, è data in Fig. 2. Vediamo ora come sia possibile, grazie al bilanciamento tra gravità e forza centrifuga, risalire dalla curva di rotazione alla distribuzione della massa nella galassia.

Consideriamo dapprima una stella di massa M* che abbia una distanza r dal centro inferiore al raggio del bulge. La gravità che agisce su di essa è data dell’equazione (1), in cui Mp viene sostituito da M* e Ms da M(r), ovvero dalla massa del bulge compresa fino alla distanza r. Nella semplice ipotesi che la densità di stelle ρ sia costante nel bulge, si ottiene ovviamente M(r) = (4π/3)ρr3. Sostituendo Mp con M* anche nell’equazione (2), e uguagliando le forze gravitazionale e centrifuga, come nel caso del Sistema solare, si ottiene V = Kr, dove la costante questa volta vale K = [(4π/3)Gρ] ½. Dunque, all’interno del bulge la velocità delle stelle aumenta con la loro distanza dal centro. Questo andamento è chiaramente visibile nel primo tratto della curva di rotazione che effettivamente cresce linearmente con r.

Per le stelle con raggi orbitali maggiori del raggio del bulge, ci si aspetta che le velocità si comportino keplerianamente perché la situazione è simile a quella del Sistema planetario, con il bulge al posto del Sole e le stelle sul disco al posto dei pianeti. Dal momento che la curva di rotazione invece è piatta, è necessario ipotizzare che la massa che origina la gravità avvertita dalle stelle non sia concentrata al centro ma abbia un andamento radiale del tipo M(r) µ r [1]. In tal caso, infatti, dall’equazione (1) abbiamo Fg µ 1/r e, imponendo la solita uguaglianza con la forza centrifuga ‑ equazione (2) ‑ otteniamo effettivamente V = costante, ovvero una velocità indipendente da r, come osservato.

All’interno di una sfera la cui massa cresca linearmente con il raggio, come ipotizzato più sopra, la materia deve essere distribuita con una densità il cui andamento radiale è ρ µ 1/r2. Infatti, dal momento che il volume sferico è proporzionale al cubo del raggio (V µ r3) e la massa è data dal prodotto della densità per il volume, si ottiene proprio M(r) = ρV µ r.

In conclusione, le galassie si trovano all’interno di un alone sferico di materia, molto più esteso del disco stellare e la cui densità decresce come l’inverso del quadrato della distanza. La forza di gravità esercitata da questo alone è assai superiore a quella esercitata dal bulge. In effetti, si valuta che la massa di quest’alone invisibile possa arrivare a essere dieci volte maggiore di quella stellare visibile. Non sappiamo ancora da cosa sia composta questa materia oscura, ma si ritiene che non sia materia ordinaria (ossia composta da protoni e neutroni) ma “esotica”, ovvero composta da particelle elementari non ancora osservate in laboratorio, ma previste dai fisici della materia.

Proprio l’elusiva natura della materia oscura ha indotto alcuni (pochi) astrofisici a negarne l’esistenza, e spiegare la costanza della curva di rotazione tramite la teoria mond (MOdified Newtonian Dynamics). Dal momento che non è mai stato possibile verificare la classica formula per la gravità di Newton per distanze superiori alle dimensioni del Sistema solare (dove funziona molto bene), si ipotizza che a grandi distanze la gravità decresca come l’inverso della distanza, Fg µ 1/r, piuttosto che come l’inverso del quadrato di questa (equazione (1)). In questo caso, l’uguaglianza tra gravità e forza centrifuga dà luogo effettivamente a una curva di rotazione piatta.

 

Home
Spigolature

 

Livello
Base

 


[1] Il simbolo µ non indica uguaglianza ma proporzionalità. Ad esempio, un espressione del tipo Fg µ 1/r2 non ci dice il valore della forza, ma esprime la proporzionalità tra questa e l’inverso del quadrato della distanza: in altri termini, descrive come la forza dipende dalla distanza.