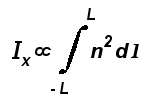Il gas intergalattico contenuto negli ammassi di galassie
possiede temperature dell’ordine 107<T<108
K, ed è quindi altamente ionizzato.
Gli elettroni sono dunque slegati dai nuclei e si muovono
liberamente. E' noto dall’elettromagnetismo
che una particella carica emette radiazione ogni volta che viene
accelerata. Pertanto un elettrone emette radiazione ogni volta che
"urta" uno ione, ovvero passa sufficientemente vicino ad un nucleo
atomico: in questo caso, infatti, l’elettrone
deflette dalla propria orbita rettilinea a causa dell’accelerazione
dovuta alla forza elettrica che si esercita tra nucleo ed elettrone.
Maggiore è il numero di urti nell’unità di
tempo, maggiore è l’intensità della radiazione
emessa.
Se la densità degli ioni è pari ad ni, questo significa
che, all’interno di un cm3, ogni
singolo elettrone emette una quantità di radiazione proporzionale a ni
urti.
La radiazione totale si ottiene moltiplicando per il
numero totale n~ni degli elettroni
presenti nel cm3, e risulta dunque proporzionale al quadrato della
densità, n2.
Finalmente, l’intensità
totale di radiazione proveniente dal gas dell’ammasso
lungo la linea di vista si ottiene sommando i contributi di tutti gli
elementi di volume allineati sul diametro dell’ammasso
lungo tale direzione:
|
I x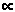 n2 L n2 L
|
( 1 )
|
dove L rappresenta il raggio dell’ammasso (assunto sferico).
Questa formula è stata ottenuta assumendo una
distribuzione uniforme di gas all’interno dell’ammasso. Una simile assunzione è
irrealistica perché il gas tende a concentrarsi verso il centro dell’ammasso della galassia e la densità è dunque
una funzione decrescente del raggio L dell’ammasso.
La formula corretta è dunque:
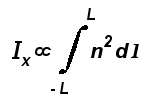
Tuttavia a noi qui preme
evidenziare la logica generale, trascurando le difficoltà tecniche, e nel
seguito faremo riferimento all'equazione (1).
Il pedice x nel simbolo dell’intensità
sta ad indicare che, a causa dell’alta
temperatura degli elettroni, la radiazione viene emessa nell’intervallo
delle frequenze dei raggi X.
Ma gli elettroni del gas
intergalattico, oltre a collidere con gli ioni emettendo radiazione X,
interagiscono con i fotoni della radiazione cosmica di fondo.
Data la loro elevata temperatura, gli elettroni, urtando i fotoni, sono in
grado di comunicare a questi ultimi una frazione della propria energia
tramite un processo detto effetto Compton inverso.
Entriamo un poco più nel dettaglio di questo fenomeno.
Le particelle di un gas ad una certa temperatura non hanno tutte la stessa
velocità, ovvero la stessa energia cinetica. Alcune saranno più lente
ed altre più veloci, e la temperatura dà una misura dell’energia
media delle particelle. Analogamente, un "gas" di
fotoni ad una certa temperatura (quale la radiazione cosmica) non è composto
da fotoni tutti della stessa energia, ovvero della stessa frequenza (essendo l’energia di un fotone pari a E=h , dove h è la costante di Plank
e , dove h è la costante di Plank
e  la frequenza). la frequenza).
|
|
|
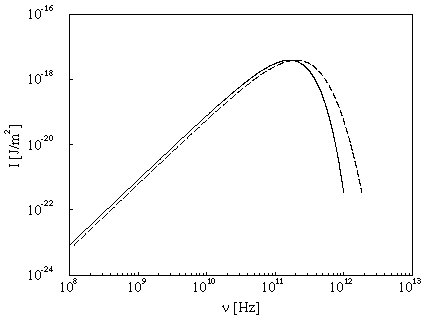
Figura 1
La distribuzione spettrale della
radiazione cosmica di fondo (linea
continua) e la distorsione
dovuta all’effetto Sunyaev-Zel’dovich.
|
Alcuni avranno frequenze minori, ed altri maggiori (la
curva continua nella figura 1 mostra come sono distribuiti i fotoni in
funzione della frequenza, ovvero il numero di fotoni di ogni frequenza
presenti in un cm3).
Succede allora che, urtando con gli elettroni, i fotoni
meno energetici acquistano energia aumentando la propria frequenza, mentre il
contrario accade per i fotoni di alta frequenza. I due effetti tuttavia
non si bilanciano, e il risultato finale netto è una diminuzione di fotoni a
basse frequenze ed un aumento alle alte frequenze (linea tratteggiata nella
figura 2).
La frequenza critica a cui l’effetto
si inverte è pari a circa 217 GHz (1 Ghz=109 Hz) e cade nell’intervallo delle onde radio. I
radiotelescopi operano in genere a frequenze inferiori (decine di GHz) e
percepiscono dunque la radiazione di fondo nell’intervallo
di frequenze in cui l’effetto Compton inverso opera
un decremento nel numero di fotoni, e dunque nell’intensità
della radiazione di fondo. Pertanto, misurando l’intensità della radiazione di fondo a queste
frequenze in direzione di un ammasso di galassie, essa risulterà diminuita di
una quantità  I
rispetto alla stessa misurata lungo una direzione che non intercetta alcun
ammasso. I
rispetto alla stessa misurata lungo una direzione che non intercetta alcun
ammasso.
Ovviamente, in analogia a quanto detto prima, questo
decremento è proporzionale al prodotto del numero di elettroni e di fotoni e
alla profondità dell’ammasso.
Dal momento che la radiazione di fondo è omogenea ed
isotropa, il numero di fotoni è sempre lo stesso in ogni direzione, e può
essere considerato costante.
Pertanto otteniamo:
|
 I I 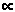 n L n L
|
( 2 )
|
Con osservazioni congiunte di raggi X e onde radio è
possibile misurare Ix
e  I
e risolvere il sistema di equazioni (1) - (2) ricavando sia la densità n
del gas intergalattico che il diametro L dell’ammasso. I
e risolvere il sistema di equazioni (1) - (2) ricavando sia la densità n
del gas intergalattico che il diametro L dell’ammasso.
Di conseguenza, si ricava anche la massa del gas M 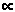 nL3. nL3.
Inoltre, dall’immagine ai
raggi X del gas caldo è possibile misurare l’angolo 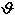 da esso sotteso sulla sfera
celeste. da esso sotteso sulla sfera
celeste.
Ma questo angolo è pari a 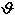 = L / = L / 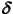 ,
dove ,
dove 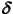 è la distanza dell’ammasso.
Quest’ultima può dunque essere ricavata una
volta che sia stato ottenuto in precedenza il valore di L. è la distanza dell’ammasso.
Quest’ultima può dunque essere ricavata una
volta che sia stato ottenuto in precedenza il valore di L.
La misura delle distanze
degli ammassi è molto importante a livello cosmologico per la determinazione
della costante di Hubble Ho che, com’è
noto, dà una misura del tasso di espansione dell’universo
e della sua età.
La legge di Hubble stabilisce che le galassie si allontanano con una velocità
v proporzionale alla loro distanza D:
v=HoD.
La velocità di allontanamento degli ammassi si ottiene, come al solito,
tramite l’effetto Doppler: la radiazione
proveniente dagli ammassi è spostata a lunghezze d’onda
tanto maggiori quanto maggiore è la velocità di allontanamento v.
Da osservazioni spettroscopiche degli ammassi si misura dunque questo
spostamento ricavando la loro velocità.
In congiunzione con la determinazione della distanza tramite l’effetto Sunyaev-Zel’dovich,
si risale infine alla costante di Hubble Ho=v/D.
L’età dell’universo,
dell’ordine di (2/3) Ho-1,
risulta essere compresa nell’intervallo 10 -16
miliardi di anni, in buon accordo con stime ottenute tramite tecniche
diverse.
|