| Dall’elettromagnetismo
classico sappiamo che la potenza W generata da un elettrone,
ovvero l’energia emessa nell’unità di tempo, è data da
W = 2e2a2/3c3
dove e ed a
sono la carica e l’accelerazione dell’elettrone, e c = 3
x 1010 cm/s è la velocità della luce. In questa
formula tutte le quantità sono costanti tranne l’accelerazione.
Accelerazioni diverse danno luogo a radiazione con caratteristiche diverse.
Se un elettrone oscilla avanti ed indietro con una frequenza  ,
emette un’onda elettromagnetica di pari frequenza; più in generale,
se un elettrone subisce una variazione di velocità ,
emette un’onda elettromagnetica di pari frequenza; più in generale,
se un elettrone subisce una variazione di velocità  v
in un tempo caratteristico t, ovvero un’accelerazione a~ v
in un tempo caratteristico t, ovvero un’accelerazione a~ v/t
, le onde emesse avranno frequenze dell’ordine di v/t
, le onde emesse avranno frequenze dell’ordine di  ~1/t
. ~1/t
.
Dal tipo di radiazione osservata si
può risalire alle condizioni della materia che l’ha emessa.
Presentiamo qui tre tipi di meccanismi
di irraggiamento:
1. la radiazione
termica prodotta da elettroni con velocità molto inferiore
a c , descritta dall’elettromagnetismo classico;
2. la radiazione
di sincrotrone generata da elettroni con velocità confrontabili
a quella della luce e accelerati dalla presenza di un campo magnetico in
cui si manifestano effetti dovuti alla teoria della relatività;
3. la emissione
di righe prodotta da elettroni all’interno di un atomo, descrivibile
mediante la meccanica quantistica.
1. Emissione
termica
Un elettrone con velocità v che passa ad una
distanza r da un nucleo atomico di carica Ze (dove Z è
il numero atomico del nucleo) sperimenta la forza di Coulomb Fe
= Ze2/r2 e subisce un’accelerazione a = Fe
/ m in un tempo dell’ordine di t = r / v.
Viene dunque emessa una potenza
w = 2e2a2
/ 3c3 = 2Z2 e6 / 3m2c3r4
ad una frequenza 1/t = v/r.
Sommando i contributi di tutti gli
incontri tra ioni ed elettroni che avvengono a diverse distanze e con diverse
velocità, si ottiene la potenza totale emessa dal plasma e la sua
distribuzione spettrale, ovvero la sua distribuzione in frequenza. Risulta
che la potenza totale emessa da un volume unitario di plasma cade nel dominio
delle onde radio (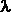 = 2 = 2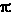 c
/ c
/  = 1-10
cm) ma non dipende dalla frequenza (viene cioè emessa la stessa
quantità di energia ad ogni frequenza) ed è proporzionale
a = 1-10
cm) ma non dipende dalla frequenza (viene cioè emessa la stessa
quantità di energia ad ogni frequenza) ed è proporzionale
a
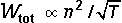
dove n e T
rappresentano, rispettivamente, il numero di elettroni per unità
di volume e la loro temperatura (che dà una misura della loro velocità).
Quando per altra via sono disponibili anche informazioni diverse (come,
ad esempio, le dimensioni della sorgente) è possibile risalire alla
densità ed alla temperatura del gas.
2. Emissione
di sincrotrone
Un elettrone che ruota attorno alle linee di un campo magnetico
B
sperimenta la forza di Lorentz FL = e B v / c
e subisce un’accelerazione a = FL/m .
Come vedremo, nel caso della radiazione di sincrotrone gli effetti
relativistici sono importanti. È conveniente allora considerare
l’impulso (o quantità di moto) p = mv dell’elettrone
piuttosto che la semplice velocità v per estendere con facilità
i risultati ottenuti al caso relativistico in cui v ~ c .
Pertanto possiamo scrivere a = eBp / m2c
, e la potenza emessa è pari a
W = 2e2 a2
/ 3c3 = 2e4 B2 p2 / 3m4
c5.
Dalla teoria della relatività
sappiamo che, nel caso in cui la velocità dell’elettrone sia vicina
a quella della luce, il suo impulso diventa p = m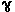 v.
v.
Il fattore 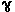 =
1 / =
1 / 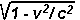 vale circa
1 per v << c , riottenendo così il valore classico
dell’impulso. vale circa
1 per v << c , riottenendo così il valore classico
dell’impulso.
Per v ~ c si ha a
= eBp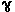 /m2c ~ eB /m2c ~ eB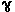 /m
e la potenza emessa diventa /m
e la potenza emessa diventa
W = 2e4 B2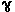 2
/ 3m2 c3. 2
/ 3m2 c3.
Dal confronto di questa formula con
quella precedente, si vede che nel caso relativistico la potenza è
un fattore (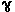 c/v)2
maggiore che nel caso classico, e questo spiega perché l’emissione
di sincrotrone è trascurabile per elettroni che hanno una velocità
molto minore di quella della luce. La frequenza di rotazione dell’elettrone
si ottiene uguagliando FL alla forza
centrifuga Fc = c/v)2
maggiore che nel caso classico, e questo spiega perché l’emissione
di sincrotrone è trascurabile per elettroni che hanno una velocità
molto minore di quella della luce. La frequenza di rotazione dell’elettrone
si ottiene uguagliando FL alla forza
centrifuga Fc =  p
. p
.
Si ottiene  = =  c/ c/ 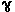 ,
dove ,
dove  c =
eB/mc è detta frequenza di Larmor. c =
eB/mc è detta frequenza di Larmor.
Contrariamente a quanto si potrebbe
pensare, a causa dell’elevata velocità dell’elettrone la frequenza
caratteristica della radiazione emessa non è dell’ordine di  ,
ma molto più alta. La radiazione viene infatti emessa in direzione
del moto all’interno di un cono di apertura angolare ,
ma molto più alta. La radiazione viene infatti emessa in direzione
del moto all’interno di un cono di apertura angolare 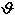 ~ 2
~ 2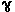 -1
che si riduce all’aumentare della velocità dell’elettrone. -1
che si riduce all’aumentare della velocità dell’elettrone.
Proprio come nel caso di un faro,
un osservatore riceve la radiazione solo per un tempo limitato t.
Questo tempo sarebbe pari al tempo necessario all’elettrone per ruotare
di un angolo 2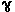 -1, -1,  t
= 2/ t
= 2/ 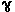 ,
se v fosse molto minore di c; in caso
contrario bisogna tenere conto che l’ultimo raggio visibile all’osservatore
viene emesso quando l’elettrone ha compiuto un percorso di circa v ,
se v fosse molto minore di c; in caso
contrario bisogna tenere conto che l’ultimo raggio visibile all’osservatore
viene emesso quando l’elettrone ha compiuto un percorso di circa v t
verso l’osservatore. t
verso l’osservatore.
La durata dell’impulso luminoso, ovvero
la differenza di tempo tra l’arrivo del primo e dell’ultimo raggio visibile,
è data allora da  t
- v t
- v  t/c = t/c =  t
(1-v/c); dato che v è vicino a c
si ha 1 - v/c ~ 1/2 t
(1-v/c); dato che v è vicino a c
si ha 1 - v/c ~ 1/2 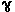 2
e in definitiva si ottiene t = 1/ 2
e in definitiva si ottiene t = 1/ 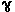 3
. 3
.
E' noto che l’energia di un’onda è
proporzionale alla sua frequenza; pertanto la frequenza dell’impulso luminoso
osservata sarà tanto maggiore quanto minore è la durata dell’impulso
perché l’osservatore possa ricevere la stessa energia in un tempo
minore. In conclusione la frequenza caratteristica della radiazione è
pari a 1/t =  c c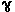 2
. 2
.
La nebulosa del Granchio contiene
un campo magnetico B = 10-4 Gauss ed è
una sorgente di sincrotrone. In questo caso  c~
1900 Hz, ma la radiazione osservata arriva a frequenze ottiche c~
1900 Hz, ma la radiazione osservata arriva a frequenze ottiche  =
=  c c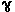 2
~ 3.8x1015 Hz, confermando la presenza di elettroni relativistici
con 2
~ 3.8x1015 Hz, confermando la presenza di elettroni relativistici
con 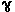 ~ 2x106 . ~ 2x106 .
3. Emissione
di riga
Dal momento che l’atomo è un sistema stabile, la meccanica
quantistica ammette che vi siano orbite determinate lungo cui l’elettrone
può ruotare attorno al nucleo senza emettere. L’energia E
dell’elettrone in orbita ad una distanza r attorno ad
un nucleo atomico è data dalla somma della sua energia cinetica
T=0.5 mv2 e potenziale U=-Ze2/r;
dal momento che la forza centrifuga Fc
pareggia
la forza attrattiva elettrostatica Fe,
mv2/r=Ze2/r2, in definitiva
si ottiene il noto risultato E =T+U= -0.5 Ze2 / r.
In un atomo eccitato l’elettrone è posizionato su un’orbita
più esterna, ad un raggio r' > r:
Questa è però una situazione di breve durata perché
l’elettrone tende a ricadere in basso, sull’orbita di minimo raggio. In
questo passaggio l’elettrone si libera dell’energia di eccitazione mediante
l’emissione di radiazione la cui energia, com’è noto, è proporzionale
alla frequenza tramite una costante 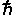 =
h / 2 =
h / 2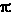 , dove h
è la costante di Planck. , dove h
è la costante di Planck.
Si ottiene pertanto 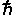  = E'-E = 0.5 Ze2 (1/r - 1/r').
= E'-E = 0.5 Ze2 (1/r - 1/r').
Le osservazioni ci dicono che un atomo eccitato emette radiazione
a certe frequenze  = =  1(1/n2
- 1/n'2), dove n ed n' sono numeri interi
e 1(1/n2
- 1/n'2), dove n ed n' sono numeri interi
e  1
è una costante. 1
è una costante.
Se ne deduce che il raggio delle orbite permesse è "quantizzato"
secondo la regola
r = ron2 .
n è detto "numero quantico" ed ro
è il cosiddetto raggio di Bohr; esso rappresenta il raggio minimo
e dà un’idea delle dimensioni di un atomo.
Evidentemente si ha  1
= 0.5 Ze2 / 1
= 0.5 Ze2 / 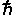 ro. ro.
È possibile ed istruttivo ottenere
il valore di ro mediante semplici
considerazioni di elettromagnetismo classico.
Se fissiamo l’attenzione per una transizione
in cui n' = n+1 e n >> 1
si ottiene
una radiazione di frequenza  =
= 1(1/n2
- 1/n'2)~2 1(1/n2
- 1/n'2)~2  1
/ n3
che, classicamente, deve coincidere con la frequenza di rotazione
dell’elettrone 1
/ n3
che, classicamente, deve coincidere con la frequenza di rotazione
dell’elettrone  2
= Ze2 / mr3 che si ottiene dall’uguaglianza
Fe
= Fc . Dall'uguaglianza tra la frequenza di rotazione
e quella della radiazione otteniamo finalmente ro = 2
= Ze2 / mr3 che si ottiene dall’uguaglianza
Fe
= Fc . Dall'uguaglianza tra la frequenza di rotazione
e quella della radiazione otteniamo finalmente ro = 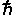 2
/ Ze2 m. 2
/ Ze2 m.
Nel caso dell’atomo di idrogeno Z
= 1 e ro = 5.3 10-9
cm. La possibilità di seguire un approccio semiclassico per n
>>1 è assicurata dal "principio di corrispondenza"
che afferma che un sistema quantistico diventa simile all’analogo classico
per alti valori del numero quantico n.
|