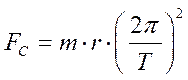|
|
|
|
|
|
|
|
|
La massa delle stelle
Claudio
Elidoro
|
Volendo andare un po’ in
profondità in quanto si è detto a proposito della massa di una stella, il
primo passo può essere quello di chiarire come mai una stella di massa
maggiore avrà un’esistenza più breve. Precisiamo subito che quanto stiamo per
dire è valido per le stelle di sequenza principale, le altre sono troppo
agitate per farci due conti in tranquillità. In prima battuta
possiamo dire che la vita di una stella dipende dal rapporto tra le sue
scorte energetiche (cioè la sua massa) e il consumo di queste scorte (cioè la
produzione di energia, dunque la sua luminosità). In simboli avremo che t »
M / L (1) dove con t si è indicato il tempo di vita di una stella, con M la massa e con L la luminosità. Nel 1926, Sir Arthur
Stanley Eddington aveva calcolato che per garantire l’equilibrio di una
stella la sua luminosità doveva essere proporzionale al cubo della sua massa.
Lo studio sistematico delle stelle di sequenza principale ha consentito di
scoprire che la relazione di proporzionalità tra la luminosità e la massa è
del tipo L µ
M a (2) dove a è compreso tra 3 e 4, dunque in
ottimo accordo con le previsioni di Eddington. Per completezza bisogna
dire che il valore di a
non è fisso, ma varia leggermente con la massa. Questo fatto, comunque, non
compromette il ragionamento che stiamo facendo. Se ora sostituiamo
l’espressione della luminosità come appare nella (2) nella espressione (1)
introducendo per a
il valore simbolico di 3,5 otteniamo t µ
1 / M 2,5 (3) Espressione che ci
conferma la correttezza dell’affermazione da cui siamo partiti, vale a dire
che la durata della vita di una stella è inversamente proporzionale alla sua
massa. Giusto per fare due
conti, proviamo a valutare quale potrà essere la durata della vita di Vega (a
Lyrae) confrontandola con il nostro Sole. Dato che
Vega ha una massa pari a 2,5 volte quella del nostro astro, vivrà per un tempo
pari a (1/2,5)2,5 = 1/10
della durata del Sole. Se, dunque, per il Sole si ipotizza una vita di circa
9 miliardi di anni, Vega brillerà per meno di un miliardo di anni. Il secondo passo di
questo approfondimento è provare a ripercorrere i passaggi teorici e i
calcoli che ci permettono di determinare la massa del Sole. Consideriamo un
qualsiasi pianeta in orbita intorno al Sole e le forze che si contrappongono
permettendo al pianeta di orbitare: da un lato vi è la forza gravitazionale e
dall’altro la forza centrifuga. Indicando con M la massa del Sole, con m
quella del pianeta e con r la
distanza che li separa, l’espressione della forza gravitazionale è data da:
Per quello stesso
pianeta possiamo esprimere la forza centrifuga come
L’espressione è stata
ottenuta considerando per semplicità un’orbita circolare di raggio r. Uguagliando ora le due espressioni
ed esplicitando M otteniamo
I più attenti avranno
senz’altro riconosciuto nella (6) la terza legge di Keplero. Con semplici
passaggi algebrici, infatti, si può verificare come questa espressione
indichi la proporzionalità tra i quadrati dei periodi di rivoluzione dei
pianeti e i cubi delle loro distanze medie dal Sole. Grazie a questa
espressione e utilizzando per semplicità i dati orbitali del pianeta Terra
siamo in grado di calcolare la massa del Sole. Impiegando dunque i
seguenti valori: r = 1.5 x T = 365 giorni = 3.15 x 107
s G = 6.67 x 10-11 Nm2/kg2 otteniamo che M = 2.01 x Un risultato notevole! Nonostante le notevoli
semplificazioni, infatti, abbiamo ottenuto un risultato incredibilmente
vicino al valore riportato dai libri di astronomia (1.99 x |